
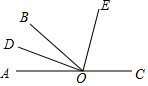
 如图,点A、O、C在同一条直线上,OD是∠AOB的平分线,OE是∠BOC的平分线,求∠DOE的度数.
如图,点A、O、C在同一条直线上,OD是∠AOB的平分线,OE是∠BOC的平分线,求∠DOE的度数. 分析 由点A、O、C在同一条直线上,OD是∠AOB的平分线,OE是∠BOC的平分线,根据角平分线的定义,可得∠DOE=$\frac{1}{2}$∠AOC,即可求得答案.
解答 解:∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠BOD=$\frac{1}{2}$∠AOB,∠BOE=$\frac{1}{2}$∠BOC,
∵点A、O、C在同一条直线上,
∴∠AOC=180°,
∴∠DOE=∠BOD+∠BOE=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOB+∠BOC)=$\frac{1}{2}$∠AOC=90°.
点评 此题考查了角平分线的性质.注意证得∠DOE=$\frac{1}{2}$∠AOC是关键.


科目:初中数学 来源: 题型:解答题
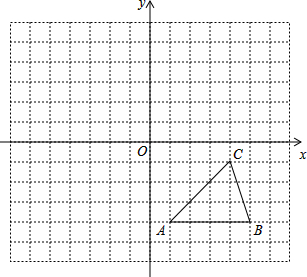 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
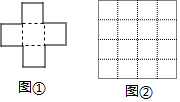 (1)一个无盖的正方体纸盒,沿某些棱剪开可以展成如图①所示的平面图形.你还能得到哪些不同的平面图形?请将它们表示出来(至少3种)
(1)一个无盖的正方体纸盒,沿某些棱剪开可以展成如图①所示的平面图形.你还能得到哪些不同的平面图形?请将它们表示出来(至少3种)查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com