【题目】甲、乙两车分别从A，B两地同时出发，沿同一条公路相向而行，相遇时甲、乙所走路程的比为
，甲、乙两车离AB中点C的路程
千米
与甲车出发时间
时的关系图象如图所示，则下列说法错误的是（ ）
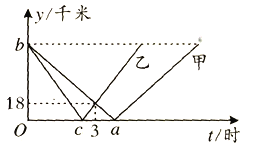
A.A，B两地之间的距离为180千米
B.乙车的速度为36千米
时
C.a的值为
D.当乙车到达终点时，甲车距离终点还有30千米
【答案】D
【解析】
根据两车相遇时甲、乙所走路程的比为2：3及两车相遇所用时间，即可求出A、B两地之间的距离；根据乙车的速度＝相遇时乙车行驶的路程÷两车相遇所用时间，进而求出乙车的速度；根据甲车的速度＝相遇时甲车行驶的路程÷两车相遇所用时间即可求出甲车的速度，然后根据时间＝两地之间路程的一半÷甲车的速度，进而求出a值；根据时间＝两地之间路程÷乙车的速度求出乙车到达终点所用时间，再求出该时间内甲车行驶的路程，用两地间的距离与甲车行驶的路程之差即可得出结论．
解：A、A、B两地之间的距离为18×2÷
＝180（千米），所以A正确；
B、乙车的速度为180
÷3＝36（千米/小时），所以B正确；
C、甲车的速度为180
=24（千米/小时），
a的值为180÷2÷24＝3.75，所以C正确；
D、乙车到达终点的时间为180÷36＝5（小时），
甲车行驶5小时的路程为24×5＝120（千米），
当乙车到达终点时，甲车距离终点距离为180﹣120＝60（千米），所以D错误．
故选：D
科目：初中数学 来源： 题型：
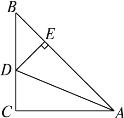
【题目】如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠BAC交BC于点D，DE⊥AB于点E，若△BDE的周长是5 cm，则AB的长为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，正六边形ABCDEF在直角坐标系的位置如图所示，A（﹣2，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过5次翻转之后，点B的坐标是______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示是一辆汽车油箱里剩油量
与行驶时间
的图像，根据图像回答下列问题：
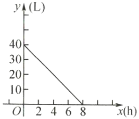
（1）汽车行驶前油箱里有______
汽油；
（2）当汽车行驶
时，油箱里还有______汽油；
（3）汽车最多能行驶______
，它每小时耗油______；
（4）油箱中剩油行驶时间之间的函数关系式是______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工厂修建了甲、乙两个水池，最大蓄水量都是1200立方米，如果甲池有水480立方米，乙池蓄满水，甲池每小时进水80立方米，乙池每小时放水100立方米.
（1）分别写出甲、乙两池的水量
与时间
的函数解析式；
（2）甲、乙两池同时进水、放水，经过几小时两个水池内的水一样多？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市举行知识大赛，A校、B校各派出5名选手组成代表队参加决赛，两校派出选手的决赛成绩如图所示．
根据图示填写下表：
平均数 | 中位数 | 众数 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
结合两校成绩的平均数和中位数，分析哪个学校的决赛成绩较好；
计算两校决赛成绩的方差，并判断哪个学校代表队选手成绩较为稳定．
查看答案和解析>>
科目：初中数学 来源： 题型：
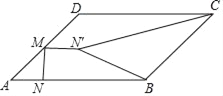
【题目】如图，在平行四边形ABCD中，∠A=45°，AB=4，AD=2
，M是AD边的中点，N是AB边上一动点，将线段M绕点M逆时针旋转90至MN′，连接N′B，N′C，则N′B+N′C的最小值是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
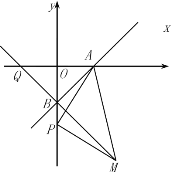
【题目】如图，平面直角坐标系中，点A、B的坐标分别为
，
，P为y轴上B点下方一点， 
，以AP为边作等腰直角△APM，其中
，点M落在第四象限．若直线MB与x轴交于点Q，则Q、M两点中，点_________（填“Q”或“M”）的坐标不随m的变化而变化，该点的坐标为______________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在梯形ABCD中，AD//BC，
,
,
,
,动点M从B点出发沿线段BC以每秒2个单位长度的速度向C运动；动点N同时从A点出发沿线段AB以每秒1个单位长度的速度向B运动，其中一点到达终点时，则两点同时停止运动.设运动的时间为t秒，当△MNB为等腰直角三角形时，t的值是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
