练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

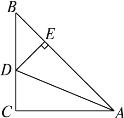
    【题目】如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠BAC交BC于点D，DE⊥AB于点E，若△BDE的周长是5 cm，则AB的长为__________．

    【答案】5cm．

    【解析】

    试题根据角平分线上的点到角的两边的距离相等可得CD=DE，然后利用“HL”证明Rt△ACD和Rt△AED全等，根据全等三角形对应边相等可得AC=AE，然后求出AB=△BDE的周长．

    试题解析：∵AD平分∠BAC，∠C=90°，DE⊥AB，

    ∴CD=DE，

    在Rt△ACD和Rt△AED中，

    ，

    ∴Rt△ACD≌Rt△AED（HL），

    ∴AE=AC，

    ∵AC=BC，

    ∴BC=AE，

    ∵△BDE的周长=BE+BD+DE=BE+BD+CD=BE+BC=BE+AE=AB，

    ∴AB=5cm．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】甲、乙两名学生在同一小区居住，一天早晨，甲、乙两人同时从家出发去同一所学校上学．甲骑自行车匀速行驶．乙步行到公交站恰好乘上一辆公交车，公交车沿公路匀速行驶，公交车的速度分别是甲骑自行车速度和乙步行速度的2倍和5倍，下车后跑步赶到学校，两人同时到达学校（上、下车时间忽略不计）．两人各自距家的路程y（m）与所用的时间x（min）之间的函数图象如图所示．

    （1）a= ，b= ．

    （2）当乙学生乘公交车时，求y与x之间的函数关系式（不要求写出自变量x的取值范围）．

    （3）如果乙学生到学校与甲学生相差1分钟，直接写出他跑步的速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点C为线段AB上一点，分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD，CB=CE，∠ACD=∠BCE=α，直线AE与BD交于点F.

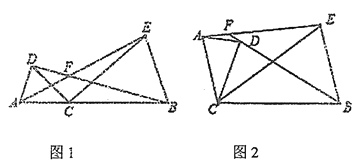
    （1）如图1所示，

    ①求证AE= BD

    ②求∠AFB (用含α的代数式表示)

    （2）将图1中的△ACD绕点C顺时针旋转某个角度(交点F至少在BD、AE中的一条线段上)，得到如图2所示的图形，若∠AFB= 150°，请直接写出此时对应的α的大小(不用证明)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形网格上有一个△DEF．

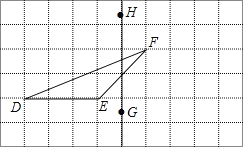
    （1）画出△DEF关于直线HG的轴对称图形（不写画法）；

    （2）画EF边上的高（不写画法）；

    （3）若网格上的最小正方形边长为1，则△DEF的面积为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC为等边三角形，点D为直线BC上的一动点(点D不与B、C重合)，以AD为边作等边△ADE(顶点A、D、E按逆时针方向排列)，连接CE．

    (1)如图1，当点D在边BC上时，求证：①BD＝CE，②AC＝CE+CD；

    (2)如图2，当点D在边BC的延长线上且其他条件不变时，结论AC＝CE+CD是否成立？若不成立，请写出AC、CE、CD之间存在的数量关系，并说明理由；

    (3)如图3，当点D在边BC的反向延长线上且其他条件不变时，补全图形，并直接写出AC、CE、CD之间存在的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（ ）

    A.带①去B.带②去C.带③去D.带①和②去

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图一段抛物线：y=﹣x（x﹣3）（0≤x≤3），记为C1，它与x轴交于点O和A1；将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3，如此进行下去，直至得到C10，若点P（28，m）在第10段抛物线C10上，则m的值为（　　）

    A. 1 B. ﹣1 C. 2 D. ﹣2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，⊙O与直线AB相切于点A，BO与⊙O交于点C，若∠BAC＝30°，则∠B等于(　　)

    A. 29° B. 30° C. 31° D. 32°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两车分别从A，B两地同时出发，沿同一条公路相向而行，相遇时甲、乙所走路程的比为，甲、乙两车离AB中点C的路程千米与甲车出发时间时的关系图象如图所示，则下列说法错误的是（ ）

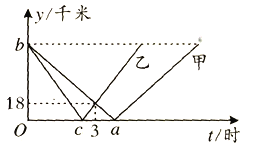
    A.A，B两地之间的距离为180千米

    B.乙车的速度为36千米时

    C.a的值为

    D.当乙车到达终点时，甲车距离终点还有30千米

    查看答案和解析>>

    同步练习册答案