
ЁОЬтФПЁПвбжЊЕуCЮЊЯпЖЮABЩЯвЛЕуЃЌЗжБ№вдACЁЂBCЮЊБпдкЯпЖЮABЭЌВрзїЁїACDКЭЁїBCE,ЧвCA=CDЃЌCB=CEЃЌЁЯACD=ЁЯBCE=ІСЃЌжБЯпAEгыBDНЛгкЕуF.
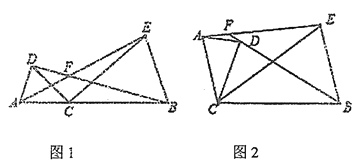
ЃЈ1ЃЉШчЭМ1ЫљЪОЃЌ
ЂйЧѓжЄAE= BD
ЂкЧѓЁЯAFB (гУКЌІСЕФДњЪ§ЪНБэЪО)
ЃЈ2ЃЉНЋЭМ1жаЕФЁїACDШЦЕуCЫГЪБеыа§зЊФГИіНЧЖШ(НЛЕуFжСЩйдкBDЁЂAEжаЕФвЛЬѕЯпЖЮЩЯ)ЃЌЕУЕНШчЭМ2ЫљЪОЕФЭМаЮЃЌШєЁЯAFB= 150ЁуЃЌЧыжБНгаДГіДЫЪБЖдгІЕФІСЕФДѓаЁ(ВЛгУжЄУї)
ЁОД№АИЁПЃЈ1ЃЉЂйМћНтЮіЃЌЂк180Ёу -ІСЃЈ2ЃЉ30Ёу
ЁОНтЮіЁП
ЃЈ1ЃЉЂйгЩЁЯACD=ЁЯBCE=ІСЃЌЕУЕНЁЯACE=ЁЯDCB=180Ёу![]() ЃЌШЛКѓЕУЕНЁїACEЁеDCBЃЌМДПЩЕУЕНAE=BDЃЛ
ЃЌШЛКѓЕУЕНЁїACEЁеDCBЃЌМДПЩЕУЕНAE=BDЃЛ
ЂкгЩЂйжЊЁїACEЁеDCBЃЌдђЁЯCAF=ЁЯCDFЃЌРћгУШ§НЧаЮФкНЧКЭЖЈРэЃЌгЩЁЯCAF+ЁЯAFB+ЁЯB=180ЁуЃЌЁЯCDF+ЁЯDCB+ЁЯB=180ЁуЃЌдђЁЯAFB=ЁЯDCB=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩЁЯAFB= 150ЁуЃЌдђЁЯEFB=![]() ЃЌгЩЁЯACD=ЁЯBCEЃЌЕУЁЯACE=ЁЯDCBЃЌШЛКѓЕУЕНЁїACEЁеЁїDCBЃЌЕУЕНЁЯAEC=ЁЯDBCЃЌдђЁЯBCE=ЁЯEFB=30Ёу.
ЃЌгЩЁЯACD=ЁЯBCEЃЌЕУЁЯACE=ЁЯDCBЃЌШЛКѓЕУЕНЁїACEЁеЁїDCBЃЌЕУЕНЁЯAEC=ЁЯDBCЃЌдђЁЯBCE=ЁЯEFB=30Ёу.
НтЃКЃЈ1ЃЉШчЭМ1ЃК
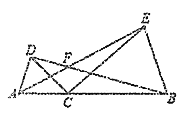
ЂйжЄУїЃКЁпЁЯACD=ЁЯBCE=ІСЃЌ
Ёр180Ёу![]() ЁЯACD=180Ёу
ЁЯACD=180Ёу![]() ЁЯBCEЃЌ
ЁЯBCEЃЌ
МДЁЯACE=ЁЯDCB=180Ёу![]() ЃЌ
ЃЌ
ЁпCA=CDЃЌCB=CEЃЌ
ЁрЁїACEЁеDCBЃЌ
ЁрAE=DBЃЛ
ЂкЁпЁїACEЁеDCBЃЌ
ЁрЁЯCAF=ЁЯCDFЃЌ
гЩШ§НЧаЮФкНЧКЭЖЈРэЃЌЕУ
ЁЯCAF+ЁЯAFB+ЁЯB=180ЁуЃЌЁЯCDF+ЁЯDCB+ЁЯB=180ЁуЃЌ
ЁрЁЯAFB=ЁЯDCB=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃК
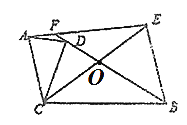
ЁпЁЯAFB= 150ЁуЃЌ
ЁрЁЯEFB=![]() ЃЌ
ЃЌ
ЁпЁЯACD=ЁЯBCEЃЌ
ЁрЁЯACD+ЁЯDCO=ЁЯBCE+ЁЯDCOЃЌ
ЁрЁЯACE=ЁЯDCBЃЌ
ЁпAC=DCЃЌCE=CBЃЌ
ЁрЁїACEЁеЁїDCBЃЌ
ЁрЁЯAEC=ЁЯDBCЃЌ
ЁпЁЯFOE=ЁЯCOBЃЌ
ЁрЁЯBCE=ЁЯEFB=30ЁуЃЌ
Ёр![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=-x2+bx+cгыxжсНЛгкЕуA(-1.0)КЭЕуB(3,0) ,гыyжсНЛгкЕуCЃЌСЌНгBCНЛХзЮяЯпЕФЖдГЦжсгкЕуEЃЌDЪЧХзЮяЯпЕФЖЅЕу.

(1)ЧѓДЫХзЮяЯпЕФНтЮіЪН
(2)жБНгаДГіЕуCКЭЕуDЕФзјБъ
(3)ШєЕуPдкЕквЛЯѓЯоФкЕФХзЮяЯпЩЯ,ЧвSЁїABP=4SЁїCDEЃЌЧѓPЕузјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФЖЏЕуЃЈЕу
ЩЯЕФЖЏЕуЃЈЕу![]() гы
гы![]() ВЛжиКЯЃЉЃЌЗжБ№вд
ВЛжиКЯЃЉЃЌЗжБ№вд![]() ЮЊБпЯђЯпЖЮ
ЮЊБпЯђЯпЖЮ![]() ЕФЭЌвЛВрзїе§
ЕФЭЌвЛВрзїе§![]() КЭе§
КЭе§![]() .
.
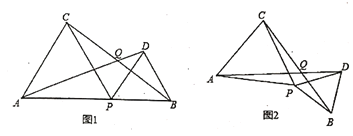
ЃЈ1ЃЉЧыФуХаЖЯ![]() гы
гы![]() гадѕбљЕФЪ§СПЙиЯЕЃПЧыЫЕУїРэгЩЃЛ
гадѕбљЕФЪ§СПЙиЯЕЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉСЌНг![]() ЃЌЯрНЛгкЕу
ЃЌЯрНЛгкЕу![]() ЃЌЩш
ЃЌЩш![]() ЃЌФЧУД
ЃЌФЧУД![]() ЕФДѓаЁЪЧЗёЛсЫцЕу
ЕФДѓаЁЪЧЗёЛсЫцЕу![]() ЕФвЦЖЏЖјБфЛЏЃПЧыЫЕУїРэгЩЃЛ
ЕФвЦЖЏЖјБфЛЏЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєЕу![]() ЙЬЖЈЃЌНЋ
ЙЬЖЈЃЌНЋ![]() ШЦЕу
ШЦЕу![]() АДЫГЪБеыЗНЯђа§зЊЃЈа§зЊНЧаЁгк
АДЫГЪБеыЗНЯђа§зЊЃЈа§зЊНЧаЁгк![]() ЃЉЃЌДЫЪБ
ЃЉЃЌДЫЪБ![]() ЕФДѓаЁЪЧЗёЗЂЩњБфЛЏЃПЃЈжЛашжБНгаДГіФуЕФВТЯыЃЌВЛБижЄУїЃЉ
ЕФДѓаЁЪЧЗёЗЂЩњБфЛЏЃПЃЈжЛашжБНгаДГіФуЕФВТЯыЃЌВЛБижЄУїЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
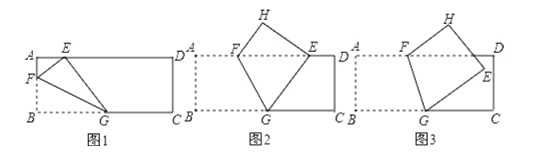
ЁОЬтФПЁПШчЭМЃЌГЄЗНаЮжНЦЌ![]() жаЃЌ
жаЃЌ![]() ЃЌНЋжНЦЌелЕўЃЌЪЙЖЅЕу
ЃЌНЋжНЦЌелЕўЃЌЪЙЖЅЕу![]() ТфдкБп
ТфдкБп![]() ЩЯЕФ
ЩЯЕФ![]() ЕуДІЃЌелКлЕФвЛЖЫ
ЕуДІЃЌелКлЕФвЛЖЫ![]() ЕудкБп
ЕудкБп![]() ЩЯ.
ЩЯ.
ЃЈ1ЃЉШчЭМ1ЃЌЕБелКлЕФСэвЛЖЫ![]() дк
дк![]() БпЩЯЧв
БпЩЯЧв![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФГЄ
ЕФГЄ
ЃЈ2ЃЉШчЭМ2ЃЌЕБелКлЕФСэвЛЖЫ![]() дк
дк![]() БпЩЯЧв
БпЩЯЧв![]() ЪБЃЌ
ЪБЃЌ
ЂйЧѓжЄЃК![]() .ЂкЧѓ
.ЂкЧѓ![]() ЕФГЄ.
ЕФГЄ.
ЃЈ3ЃЉШчЭМ3ЃЌЕБелКлЕФСэвЛЖЫ![]() дк
дк![]() БпЩЯЃЌ
БпЩЯЃЌ![]() ЕуЕФЖдгІЕу
ЕуЕФЖдгІЕу![]() дкГЄЗНаЮФкВПЃЌ
дкГЄЗНаЮФкВПЃЌ![]() ЕН
ЕН![]() ЕФОрРыЮЊ2
ЕФОрРыЮЊ2![]() ЃЌЧв
ЃЌЧв![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ЕФЖдГЦжсЮЊ
ЕФЖдГЦжсЮЊ![]() ЃЌгы
ЃЌгы![]() жсЕФвЛИіНЛЕудк
жсЕФвЛИіНЛЕудк![]() КЭ
КЭ![]() жЎМфЃЌЦфВПЗжЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлЃК
жЎМфЃЌЦфВПЗжЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлЃК
![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() Еу
Еу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЪЧИУХзЮяЯпЩЯЕФЕуЃЌдђ
ЪЧИУХзЮяЯпЩЯЕФЕуЃЌдђ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ![]() ЃЈ
ЃЈ![]() ЮЊШЮвтЪЕЪ§ЃЉЃЎ
ЮЊШЮвтЪЕЪ§ЃЉЃЎ
Цфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ

A. 2 B. 3 C. 4 D. 5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
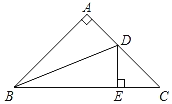
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌЁЯAЃН90ЁуЃЌBDЪЧЁЯABCЕФЦНЗжЯпЃЌDEЁЭBCгкEЃЌШєBCЃН12ЃЌдђЁїDECЕФжмГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЁЂBвдМАжБЯпlЃЌAEЁЭlЃЌДЙзуЮЊЕуEЃЎ
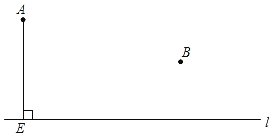
ЃЈ1ЃЉЙ§ЕуBзїBFЁЭlЃЌДЙзуЮЊЕуFЃЛ
ЃЈ2ЃЉдкжБЯпlЩЯЧѓзївЛЕуCЃЌЪЙCAЃНCBЃЛ
ЃЈвЊЧѓЃКЕкЃЈ1ЃЉЁЂЃЈ2ЃЉаЁЬтгУГпЙцзїЭМЃЌВЂдкЭМжаБъУїЯргІзжФИЃЌБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЎЃЉ
ЃЈ3ЃЉдкЫљзїЕФЭМжаЃЌСЌНгCAЁЂCBЃЌШєЁЯACBЃН90ЁуЃЌЧѓжЄЃКЁїAECЁеЁїCFBЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
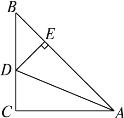
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯCЃН90ЁуЃЌACЃНBCЃЌADЦНЗжЁЯBACНЛBCгкЕуDЃЌDEЁЭABгкЕуEЃЌШєЁїBDEЕФжмГЄЪЧ5 cmЃЌдђABЕФГЄЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌе§СљБпаЮABCDEFдкжБНЧзјБъЯЕЕФЮЛжУШчЭМЫљЪОЃЌAЃЈЉ2ЃЌ0ЃЉЃЌЕуBдкдЕуЃЌАбе§СљБпаЮABCDEFбиxжсе§АыжсзїЮоЛЌЖЏЕФСЌајЗзЊЃЌУПДЮЗзЊ60ЁуЃЌОЙ§5ДЮЗзЊжЎКѓЃЌЕуBЕФзјБъЪЧ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com