
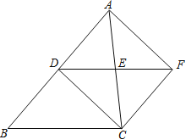
【题目】如图,在△ABC中,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE.
(1)求证:四边形ADCF是平行四边形.
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
【答案】(1)证明见解析(2)当∠ACB=90°,AC=BC时,四边形ADCF是正方形
【解析】
(1)利用旋转的性质得出点A、E、C三点共线,点D、E、F三点共线,且AE=CE,DE=FE,即可得出答案;
(2)首先得出CD⊥AB,即∠ADC=90°,由(1)知,四边形ADCF是平行四边形,故四边形ADCF是矩形.进而求出CD=AD即可得出答案.
(1)证明:∵△CFE是由△ADE绕点E旋转180°得到,
∴点A、E、C三点共线,点D、E、F三点共线,
且AE=CE,DE=FE,
故四边形ADCF是平行四边形.
(2)当∠ACB=90°,AC=BC时,四边形ADCF是正方形.
理由如下:在△ABC中,∵AC=BC,AD=BD,
∴CD⊥AB,即∠ADC=90°.
而由(1)知,四边形ADCF是平行四边形,
∴四边形ADCF是矩形.
又∵∠ACB=90°,
∴![]() ,
,
故四边形ADCF是正方形.


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O为坐标原点,抛物线y=a(x﹣h)2﹣4(a>0)与x轴分别交于原点O、A两点,点A在x轴的正半轴上,顶点为D,直线y= ![]() x交抛物线于B点,过B作BE∥x轴交抛物线另一点E,交对称轴于F.
x交抛物线于B点,过B作BE∥x轴交抛物线另一点E,交对称轴于F.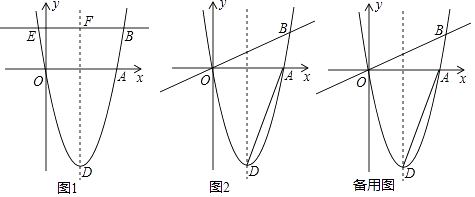
(1)当DF=4a时,求BE的长.
(2)如图2,连AD,连接AD绕点A旋转交直线OB于点G,点D的对应点为G,当OG=2时,求a的值;
(3)在(2)的条件下,当0<a<1时,以OB为直径作圆交x轴下方抛物线于点P,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
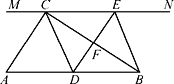
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a、图b是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,点A、B在小正方形的顶点上.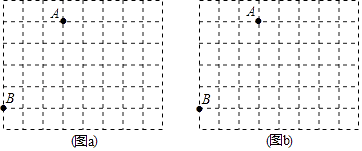
(1)在图a中画出△ABC(点C在小正方形的顶点上),使△ABC是等腰三角形且△ABC为钝角三角形;
(2)在图b中画出△ABD(点D在小正方形的顶点上),使△ABD是等腰三角形,且tan∠ABD=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题: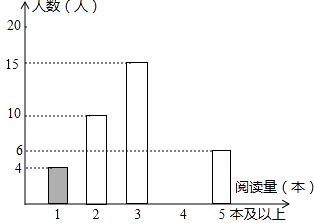
(1)求被抽查学生人数并直接写出被抽查学生课外阅读量的中位数;
(2)将条形统计图补充完整;
(3)若规定:假期阅读3本及3本以上课外书者为完成假期作业,据此估计该校1500名学生中,完成假期作业的有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司员工的月工资如下表:
员工 | 经理 | 副经理 | 职员A | 职员B | 职员C | 职员D | 职员E | 职员F | 职员G |
月工资/元 | 4800 | 3500 | 2000 | 1900 | 1800 | 1600 | 1600 | 1600 | 1000 |
则这组数据的平均数、众数、中位数分别为( )
A. 2200元 1800元 1600元 B. 2000元 1600元 1800元
C. 2200元 1600元 1800元 D. 1600元 1800元 1900元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市举行店庆活动,对甲、乙两种商品实行打折销售,打折前,购买2件甲商品和3件乙商品需要180元;购买1件甲商品和4件乙商品需要200元,而店庆期间,购买10件甲商品和10件乙商品仅需520元,这比打折前少花多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com