
����Ŀ��ijѧУΪ�˽�ѧ���Ŀ����Ķ����������ʦ�����鲿��ѧ��������������ڼ�Ŀ����Ķ�������ͳ�Ʒ��������Ƴ���ͼ��ʾ����������ͳ��ͼ����֪����ѧ��������ڼ��Ķ���Ϊ2��������ռ�����������20%��������������Ϣ������������⣺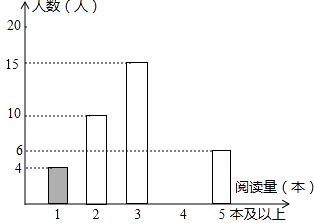
��1�����ѧ��������ֱ��д�������ѧ�������Ķ�������λ����
��2��������ͳ��ͼ����������
��3�����涨�������Ķ�3����3�����Ͽ�������Ϊ��ɼ�����ҵ���ݴ˹��Ƹ�У1500��ѧ���У���ɼ�����ҵ���ж�����ѧ����
���𰸡�
��1���⣺�����ѧ������Ϊ��10��20%=50���ˣ�����λ����3����
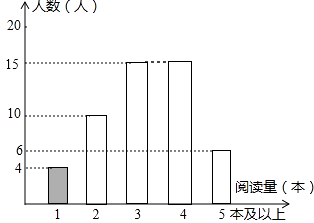
��2���⣺�Ķ���Ϊ4��������Ϊ��50��4��10��15��6=15���ˣ�����ȫ����ͳ��ͼ��ͼ��
��3���⣺ ![]() ��1500=1080��������
��1500=1080��������
�𣺹��Ƹ�У1500��ѧ���У���ɼ�����ҵ����1080��ѧ����
����������1������λ���Ķ���ɵó���λ���ǵ�25��26����������ƽ�������������������ڵ�3�飨3�����ڣ������λ������3������2�������4�������Ϊ15�ˣ�����С�����μ���;��3�� �����������Կ��Թ�����������ԣ�������1500������������Ӧ�ٷֱ�.
�����㾫����������Ĺؼ�����������λ�������������֪ʶ��������λ����Ψһ�ģ��������ݵ�����λ���йأ������ܳ�������������ݣ���������һ����Ҳ���ܶ������һ�������������е�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�������ѧϰ���θ�ʽʱ��ʽ��![]() �����壬��x��0��ʽ��
�����壬��x��0��ʽ��![]() �����壬��x��0����ʽ��
�����壬��x��0����ʽ��![]() +
+![]() �����壬��x��ȡֵ��Χ. ����������ת��Ϊ����ʽ����������������x�IJ���ʽ��x��0��x��0�Ľ⼯�����������ʽ�飬��x=0. ����������������ѧ��������������⣺
�����壬��x��ȡֵ��Χ. ����������ת��Ϊ����ʽ����������������x�IJ���ʽ��x��0��x��0�Ľ⼯�����������ʽ�飬��x=0. ����������������ѧ��������������⣺
��1��ʽ��![]() +
+![]() �����壬��x��ȡֵ��Χ��
�����壬��x��ȡֵ��Χ��
��2����֪y=![]() +
+![]() -3����
-3����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����,��ʦ��ʾij�����������ֱ�����:

(1)�ӱ��п��Կ���,��һ�������ٷ�,ʤһ�������ٷ֣�
(2)�����æ�������ʤ�˶��ٳ�?
(3)����α�����,һ����ʤ���ܻ����ܲ��ܵ������ĸ����ܻ���?
(4)�ڼ�����ӡ�����ʤ�����ε�ʱ��,��ʦ��û��ͬѧ�Ǽ������������˵���˴𰸣���ʦ����˵:������ͨ���ҵ�������ʤ��֮���������ϵ���������������˵�����еİ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�ı߳�Ϊ4����E��F�ֱ��ڱ�BC��CD�ϣ���EAF=45�㣬��AEAF= ![]() ����EF�ij�Ϊ ��
����EF�ij�Ϊ �� 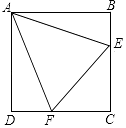
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
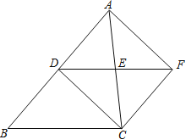
����Ŀ����ͼ������ABC�У���D��E�ֱ��DZ�AB��AC���е㣬����ADE�Ƶ�E��ת180���õ���CFE��
��1����֤���ı���ADCF��ƽ���ı��Σ�
��2������ABC����ʲô����ʱ���ı���ADCF�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����ABCD�У�AD=6��AB=4����E��G��H��F�ֱ���AB��BC��CD��AD�ϣ���AF��CG��2��BE��DH��1����P��ֱ��EF��GH֮������һ�㣬����PE��PF��PG��PH�����PEF�͡�PGH�������Ϊ�� ��

A. 5 B. 6
C. 7 D. 8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��һ���Խ���ƽ��һ��Խǵ��ı��ν������Σ�
̽������1����ͼ1���ı���ABCD�У�AB��BC��AD��DC����֤���ı���ABCD�����Σ�
��2�����й������ε����ʱ�����ȷ���� ����������Ϊ��ȷ��������ں����ϣ�
�����εĶԽ����ഹֱƽ�֣� ��������������һ�ԶԽ���ȣ�
����������Գ�ͼ�Σ� �����ε�������������Խ��߳��Ļ���һ�룮
Ӧ�ã�
��3����ͼ2��������ABCD�У�AB��AD������ABC��60�㣬��ADC��30�㣬AD��4��������Խ���BD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ABΪ��O��ֱ����CDΪ��O���ң�CD��AB������B������������AD���ڵ�M������AC��BD��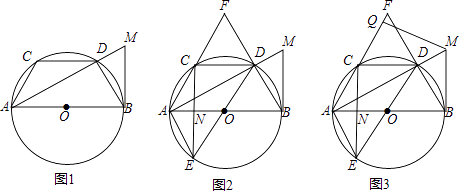
��1����ͼl����֤��AC=BD��
��2����ͼ2���ӳ�AC��BD���ڵ�F����ֱ��DE������AE��CE��CE��AB���ڵ�N����֤����AFB=2��AEN��
��3����ͼ3���ڣ�2���������£�����M��MQ��AF�ڵ�Q����MQ��QC=3��2��NE=2����QF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
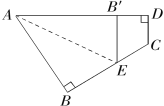
����Ŀ����ͼ��ʾ��һ���ı���ֽƬABCD����B=��D=![]() ����ֽƬ����ͼ��ʾ�۵���ʹ��B����AD���ϵ�B���㣬AE���ۺۣ�
����ֽƬ����ͼ��ʾ�۵���ʹ��B����AD���ϵ�B���㣬AE���ۺۣ�
��1�����ж�B��E��DC��λ�ù�ϵ����˵�����ɣ�
��2�������C=![]() �����AEB�Ķ�����
�����AEB�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com