
【题目】已知正方形ABCD的边长为4,点E,F分别在边BC、CD上,∠EAF=45°,若AEAF= ![]() ,则EF的长为 .
,则EF的长为 . 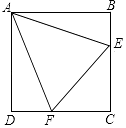
【答案】![]()
【解析】解:如图将△ABE绕点A顺时针旋转90°得到△ADM,作FH⊥AE于H.
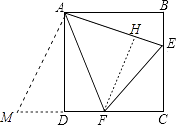
∵四边形ABCD是正方形,
∴∠DAB=90°,∵∠EAF=45°,
∴∠BAE+∠DAF=∠DAF+∠MAD=45°,
∴∠FAE=∠FAM,
在△FAE和△FAM中,
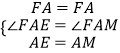 ,
,
∴△FAE≌△FAM,
∴EF=FM,S△FAE=S△FAM,
∵FH⊥AE,∠FAH=45°,
∴FH=AFsin45°= ![]() AF,
AF,
∵S△AEF= ![]() AEFH=
AEFH= ![]() AE
AE ![]() AF=
AF= ![]() AEAF=
AEAF= ![]() ,
,
∴ ![]() EFAD=
EFAD= ![]() ,
,
∴EF= ![]()
所以答案是 ![]() .
.
【考点精析】利用正方形的性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】在△ABC中,DE垂直平分AB,分别交AB,BC于点D,E,MN垂直平分AC,分别交AC,BC于点M,N.
(1)如图①,若∠BAC = 110°,求∠EAN的度数;
(2)如图②,若∠BAC =80°,求∠EAN的度数;
(3)若∠BAC = α(α ≠ 90°),直接写出用α表示∠EAN大小的代数式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.

(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= °时,四边形BFDE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2017年1月1日开始,居民生活用气阶梯价格制度正式实施,一般生活用气收费标准如下表所示,比如6口以下的户年天然气用量在第二档时,其中350立方米按![]() 收费,超过350立方米的部分按
收费,超过350立方米的部分按![]() 收费.小锋一家有五口人,他想帮父母计算一下实行阶梯价后,家里天然气费的支出情况:
收费.小锋一家有五口人,他想帮父母计算一下实行阶梯价后,家里天然气费的支出情况:
(1)如果他家2017年全年使用200立方米天然气,那么需要交多少元天然气费?
(2)如果他家2017年全年使用400立方米天然气,那么需要交多少元天然气费?
(3)如果他家2018年需要交1563元天然气费,他家2018年用了多少立方米天然气?

查看答案和解析>>
科目:初中数学 来源: 题型:
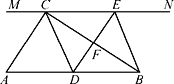
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5月13日,周杰伦2017“地表最强”世界巡回演唱会在奥体中心盛大举行,1号巡逻员从舞台走往看台,2号巡逻号从看台走往舞台,两人同时出发,分别以各自的速度在舞台与看台间匀速走动,出发1分钟后,1号巡逻员发现对讲机遗忘在出发地,便立即返回出发地,拿到对讲机后(取对讲机时间不计)立即再从舞台走往看台,结果1号巡逻员先到达看台,2号巡逻员继续走到舞台,设2号巡逻员的行驶时间为x(min),两人之间的距离为y(m),y与x的函数图象如图所示,则当1号巡逻员到达看台时,2号巡逻员离舞台的距离是米.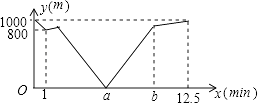
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题: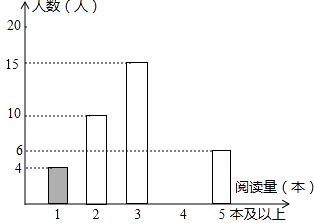
(1)求被抽查学生人数并直接写出被抽查学生课外阅读量的中位数;
(2)将条形统计图补充完整;
(3)若规定:假期阅读3本及3本以上课外书者为完成假期作业,据此估计该校1500名学生中,完成假期作业的有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真的探索。
(思考题)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
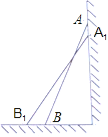
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1=![]()
而A1B1=2.5,在Rt△A1B1C中,由![]() 得方程 ,
得方程 ,
解方程得x1= ,x2= ,
∴点B将向外移动 米。
(2)解完“思考题”后,小聪提出了如下两个问题:
(问题一)在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(问题二)在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)|﹣3|+(﹣1)2016×(π﹣3.14)0﹣(![]() )﹣2+2﹣3
)﹣2+2﹣3
(2)利用乘法公式计算:20182﹣2017×2019
(3)已知2a=3,4b=5,8c=7,求8a+c﹣2b的值.
(4)已知x2﹣5x=14,求(x﹣1)(2x﹣1)﹣(x+1)2+1的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com