
【题目】小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真的探索。
(思考题)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
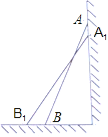
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1=![]()
而A1B1=2.5,在Rt△A1B1C中,由![]() 得方程 ,
得方程 ,
解方程得x1= ,x2= ,
∴点B将向外移动 米。
(2)解完“思考题”后,小聪提出了如下两个问题:
(问题一)在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(问题二)在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题。
【答案】(1)![]() ;0.8,﹣2.2(舍去);0.8。(2)①不会是0.9米,理由见解析②有可能。理由见解析
;0.8,﹣2.2(舍去);0.8。(2)①不会是0.9米,理由见解析②有可能。理由见解析
【解析】
解:(1)![]() ;0.8,﹣2.2(舍去);0.8。
;0.8,﹣2.2(舍去);0.8。
(2)①不会是0.9米,理由如下:
若AA1=BB1=0.9,则A1C=2.4﹣0.9=1.5,B1C=0.7+0.9=1.6,1.52+1.62=4.81,2.52=6.25,
∵![]() ,∴该题的答案不会是0.9米。
,∴该题的答案不会是0.9米。
②有可能。理由如下:
设梯子顶端从A处下滑x米,点B向外也移动x米,
则有![]() ,解得:x=1.7或x=0(舍去)。
,解得:x=1.7或x=0(舍去)。
∴当梯子顶端从A处下滑1.7米时,点B向外也移动1.7米,即梯子顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等。
(1)直接把B1C、A1C、A1B1的值代入进行解答即可。
(2)把(1)中的0.4换成0.9可知原方程不成立;设梯子顶端从A处下滑x米,点B向外也移动x米代入(1)中方程,求出x的值符合题意


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
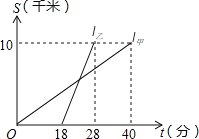
【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:
①乙比甲提前12分钟到达; ②甲的平均速度为15千米/小时;
③乙走了8km后遇到甲; ④乙出发6分钟后追上甲.
其中正确的有_____________(填所有正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连结PE、PF、PG、PH,则△PEF和△PGH的面积和为( )

A. 5 B. 6
C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一条对角线平分一组对角的四边形叫做筝形.
探究:(1)如图1,四边形ABCD中,AB=BC,AD=DC,求证:四边形ABCD是筝形;
(2)下列关于筝形的性质表述正确的是 ;(把你认为正确的序号填在横线上)
①筝形的对角线互相垂直平分; ②筝形中至少有一对对角相等;
③筝形是轴对称图形; ④筝形的面积等于两条对角线长的积的一半.
应用:
(3)如图2,在筝形ABCD中,AB≠AD,若∠ABC=60°,∠ADC=30°,AD=4,请求出对角线BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB![]() .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
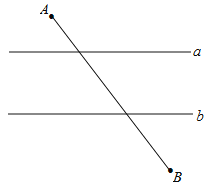
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB为⊙O的直径,CD为⊙O的弦,CD∥AB,过点B的切线与射线AD交于点M,连接AC,BD.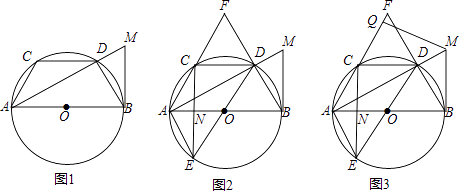
(1)如图l,求证:AC=BD;
(2)如图2,延长AC、BD交于点F,作直径DE,连接AE、CE,CE与AB交于点N,求证:∠AFB=2∠AEN;
(3)如图3,在(2)的条件下,过点M作MQ⊥AF于点Q,若MQ:QC=3:2,NE=2,求QF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人匀速从学校出发,相约在某景点见面,甲于8:00出发5分钟后,乙以 a米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s与t的关系示意图一部分如图所示.
根据图中提供的信息回答下列问题:
(1)甲行走的速度为______米/分;
(2)补齐图象,并指出甲到达景点的时刻;
(3)求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
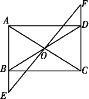
【题目】如图所示,在矩形ABCD中,O是AC与BD的交点,过点O的直线EF与AB,CD的延长线分别交于点E,F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么条件时,四边形AECF是菱形?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com