
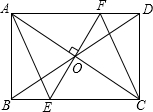
 如图,O为矩形ABCD对角线的交点,过O作EF⊥AC,分别交AD、BC于F、E,若AB=2cm,BC=4cm.
如图,O为矩形ABCD对角线的交点,过O作EF⊥AC,分别交AD、BC于F、E,若AB=2cm,BC=4cm.
|
| 3 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 10 |
| AC |
| 5 |
| 10 |
| AC |
| 5 |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
 在一条大的河流中有一形如三角形的小岛,如图,岸与小岛有一桥相连,现准备在小岛的三边上各设立一个水质取样点,水利部门在岸边设立了一个观察站,每天有专人从观察站步行去三个取样点取样,然后带去化验,请问:三个取样点应分别设在什么位置,才能使每天取样所用的时间最短?(假设行走速度不变)
在一条大的河流中有一形如三角形的小岛,如图,岸与小岛有一桥相连,现准备在小岛的三边上各设立一个水质取样点,水利部门在岸边设立了一个观察站,每天有专人从观察站步行去三个取样点取样,然后带去化验,请问:三个取样点应分别设在什么位置,才能使每天取样所用的时间最短?(假设行走速度不变)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com