
����Ŀ��(2016����������23��)
������ij��ҵ������Ӧ���������·�չ���ĺ��٣��з���һ���²�Ʒ����֪�з����������ֲ�Ʒ�ijɱ�Ϊ30Ԫ����������������y(���)�����ۼ�x(Ԫ����)�ĺ�������ʽΪ��
![]()
(1)����ҵ���۸ò�Ʒ����������ΪW(��Ԫ)����ֱ��д��������W(��Ԫ)�����ۼ�(Ԫ/��)�ĺ�������ʽ��
(2)���ò�Ʒ���ۼ�x(Ԫ/��)Ϊ����ʱ����ҵ���۸ò�Ʒ��õ����������?����������Ƕ���?
(3)����ҵ���۸ò�Ʒ��������������750��Ԫ����ȷ���ò�Ʒ���ۼ�x(Ԫ/��)��ȡֵ��Χ��
���𰸡�(1)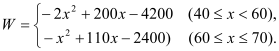 (2)���ò�Ʒ���ۼ۶�Ϊ50Ԫ����ʱ�����۸ò�Ʒ������������������Ϊ800��Ԫ��(3)Ҫʹ��ҵ���۸ò�Ʒ������������750��Ԫ���ò�Ʒ�����ۼ�x(Ԫ/��)��ȡֵ��ΧΪ45��x��55.
(2)���ò�Ʒ���ۼ۶�Ϊ50Ԫ����ʱ�����۸ò�Ʒ������������������Ϊ800��Ԫ��(3)Ҫʹ��ҵ���۸ò�Ʒ������������750��Ԫ���ò�Ʒ�����ۼ�x(Ԫ/��)��ȡֵ��ΧΪ45��x��55.
��������
���������(1)������������=����������ÿ����Ʒ������ÿ����Ʒ���ۼ�-ÿ����Ʒ�Ľ��ۣ���ֱ���г�ʽ�ӣ����ɣ���2�����ݶ��κ��������ʣ��ֱ�����������������ֵ���Ƚϼ��ɵý��ۣ���3�����ɣ�2���Ľ��ۣ��ų��ڶ���������ٸ��ݶ��κ��������ʣ��ɵ�һ�����ȷ��x��ȡֵ��Χ.
���������(1)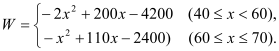
(2)��(1)֪����540��x<60ʱ��W=-2��x-50��2+800��
��-2<0��������x=50ʱ��W�����ֵ800��
��60��x��70ʱ��W=-��x-55��2+625.
��-1��0�� ����60��x��70ʱ��W��x���������С��
����x=60ʱ��W�����ֵ600��
![]()
�����ò�Ʒ���ۼ۶�Ϊ50Ԫ����ʱ�����۸ò�Ʒ������������������Ϊ800��Ԫ��
(3)��40��x��60ʱ����W=750����
-2(x-50)2+800=750,��֮����![]()
�ɺ���W=-2(x-50)2+800�����ʿ�֪��
��45��x��55ʱ��W��750��
��60��x��70ʱ��W���ֵΪ600��750.
���ԣ�Ҫʹ��ҵ���۸ò�Ʒ������������750��Ԫ���ò�Ʒ�����ۼ�x(Ԫ/��)��ȡֵ��ΧΪ45��x��55.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
��A��B�������Ϸֱ��ʾʵ��a��b��A��B����֮��ľ����ʾΪ�OAB�O.
��A��B��������һ����ԭ��ʱ���������A��ԭ�㣬��ͼ1���OAB�O���OOB�O���Ob�O���Oa-b�O��
![]()
��A��B���㶼����ԭ��ʱ����ͼ2����A��B����ԭ����ұ�
�OAB�O=�OOB�O-�OOA�O=�Ob�O-�Oa�O=![]() =�Oa-b�O��
=�Oa-b�O��
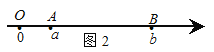
��ͼ3������A��B����ԭ�����ߣ�
�OAB�O���OOB�O-�OOA�O���Ob�O-�Oa�O=![]() =�Oa-b�O��
=�Oa-b�O��
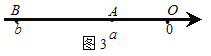
��ͼ4������A��B��ԭ������ߣ�
�OAB�O���OOB�O+�OOA�O���Oa�O+�Ob�O= ![]() =�Oa-b�O��
=�Oa-b�O��
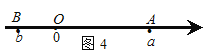
�ش��������⣺
��1�������ϱ�ʾ1��6������֮��ľ����� �������ϱ�ʾ2�ͣ�3������֮��ľ����� ��
��2������������A��ʾ������x����B��ʾ�����ǣ�4�����A��B֮��ľ����� �����OAB�O��3����ôxΪ ��
��3����x�� ʱ������ʽ![]() ��
��
��4������A��ʾ����![]() ����B���A�ľ�����10���ҵ�B�ڵ�A���Ҳ࣬����P��Qͬʱ��A��B�����������������˶�����P���ٶ���ÿ��3����λ���ȣ���Q���ٶ���ÿ��
����B���A�ľ�����10���ҵ�B�ڵ�A���Ҳ࣬����P��Qͬʱ��A��B�����������������˶�����P���ٶ���ÿ��3����λ���ȣ���Q���ٶ���ÿ��![]() ����λ���ȣ����˶������Q���P ���1����λ������д����Ҫ�������̣�
����λ���ȣ����˶������Q���P ���1����λ������д����Ҫ�������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A.2a+a2=3a3
B.a6��a2=a3
C.��a2��3=a6
D.3a2��2a=a2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016�㶫ʡ÷���е�19��)
��ͼ����֪��ƽ��ֱ������ϵ�У�![]() ������ԭ�㣬��A��2��5���ڷ���������
������ԭ�㣬��A��2��5���ڷ���������![]() ��ͼ���ϣ�һ�κ���
��ͼ���ϣ�һ�κ���![]() ��ͼ�����A�����뷴��������ͼ�����һ����ΪB��
��ͼ�����A�����뷴��������ͼ�����һ����ΪB��
��1����![]() ��
��![]() ��ֵ��
��ֵ��
��2���跴��������ֵΪ![]() ��һ�κ���ֵΪ
��һ�κ���ֵΪ![]() ����
����![]() ʱ
ʱ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
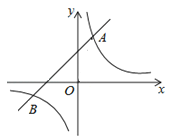
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У�ֱ��y=kx+4��x �������ύ��һ��A����y�ύ�ڵ�B����֪��OAB�����Ϊ10��������ֱ�ߵĽ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǿ��ѡ�����һ�α�ֱ����������ʻ��һ�ξ��롱�������������췽��_________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������y= -2x��ͼ���� ��
A.������һ����B.�ڶ���������C.�ڶ���һ����D.������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BE��AB���ӳ��ߣ�ָ����������е�����������������ֱ�߱���һ��ֱ�������γɵģ�������ʲô�ǣ�
��1����A�͡�D��
��2����A�͡�CBA��
��3����C�͡�CBE��
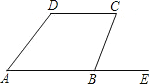
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com