
����Ŀ���Ķ�������ϣ�
��A��B�������Ϸֱ��ʾʵ��a��b��A��B����֮��ľ����ʾΪ�OAB�O.
��A��B��������һ����ԭ��ʱ���������A��ԭ�㣬��ͼ1���OAB�O���OOB�O���Ob�O���Oa-b�O��
![]()
��A��B���㶼����ԭ��ʱ����ͼ2����A��B����ԭ����ұ�
�OAB�O=�OOB�O-�OOA�O=�Ob�O-�Oa�O=![]() =�Oa-b�O��
=�Oa-b�O��
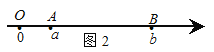
��ͼ3������A��B����ԭ�����ߣ�
�OAB�O���OOB�O-�OOA�O���Ob�O-�Oa�O=![]() =�Oa-b�O��
=�Oa-b�O��
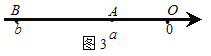
��ͼ4������A��B��ԭ������ߣ�
�OAB�O���OOB�O+�OOA�O���Oa�O+�Ob�O= ![]() =�Oa-b�O��
=�Oa-b�O��
�ش��������⣺
��1�������ϱ�ʾ1��6������֮��ľ����� �������ϱ�ʾ2�ͣ�3������֮��ľ����� ��
��2������������A��ʾ������x����B��ʾ�����ǣ�4�����A��B֮��ľ����� �����OAB�O��3����ôxΪ ��
��3����x�� ʱ������ʽ![]() ��
��
��4������A��ʾ����![]() ����B���A�ľ�����10���ҵ�B�ڵ�A���Ҳ࣬����P��Qͬʱ��A��B�����������������˶�����P���ٶ���ÿ��3����λ���ȣ���Q���ٶ���ÿ��
����B���A�ľ�����10���ҵ�B�ڵ�A���Ҳ࣬����P��Qͬʱ��A��B�����������������˶�����P���ٶ���ÿ��3����λ���ȣ���Q���ٶ���ÿ��![]() ����λ���ȣ����˶������Q���P ���1����λ������д����Ҫ�������̣�
����λ���ȣ����˶������Q���P ���1����λ������д����Ҫ�������̣�
���𰸡���1��5 ��5��2��![]() ��-7��-1��3��-4��3��4��
��-7��-1��3��-4��3��4��![]() ��
��![]()
�����������������
��1�����Ķ��������ݿ�֪������������������A��B����ʾ�����ֱ�Ϊ��a��b����A��B�����ľ���![]() ���ɴ˿ɼ��㱾��𰸣�
���ɴ˿ɼ��㱾��𰸣�
��2��ͬ��1���ɽ�õ�һ�յĴ������ݣ�1���еĹ�ʽ�;���ֵ�����壬���з��̽�õڶ��յĴ𰸣�
��3�����Ķ����Ͽ�֪��![]() ��ʾ�������ϱ�ʾ����x���ĵ㵽��ʾ����-2��������1����������ľ���֮�͵���7�����Ƿ�
��ʾ�������ϱ�ʾ����x���ĵ㵽��ʾ����-2��������1����������ľ���֮�͵���7�����Ƿ�![]() ��
��![]() ��
��![]() �������������ʽ��
�������������ʽ��![]() �Ϳ������x����ֵ��
�Ϳ������x����ֵ��
��4���������֪����A��ʾ����Ϊ��-1������B��ʾ�����ǡ�9����������֪�ɵã�![]() ��
��![]() ����P��Q���1����λ����ʱ��Ҫ�ֵ�Q�ڵ�P�ұߺ͵�Q�ڵ�P���������������ۣ���ͼ1��ͼ2���г����̿���⣻
����P��Q���1����λ����ʱ��Ҫ�ֵ�Q�ڵ�P�ұߺ͵�Q�ڵ�P���������������ۣ���ͼ1��ͼ2���г����̿���⣻
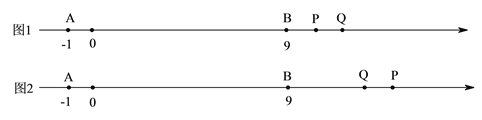
���������
��1����![]() ��
��
�����ն�Ӧ�5����
��2��������������A��ʾ������x����B��ʾ�����ǣ�4��
��![]() ��
��
����![]() ��
��
��![]() ����
����![]() �������
�������![]() ��
��![]() ��
��
��3�����Ķ����Ͽ�֪��![]() ��ʾ�������ϱ�ʾ����x���ĵ㵽��ʾ����-2��������1����������ľ���֮�͵���7������Ҫ���Ƿ�
��ʾ�������ϱ�ʾ����x���ĵ㵽��ʾ����-2��������1����������ľ���֮�͵���7������Ҫ���Ƿ�![]() ��
��![]() ��
��![]() ������������ۣ�
������������ۣ�
�ٵ�![]() ʱ��
ʱ��![]() �ɻ�Ϊ��
�ɻ�Ϊ��![]() ����ã�
����ã�![]() ��
��
����![]() ʱ��
ʱ��![]() �ɻ�Ϊ��
�ɻ�Ϊ��![]() ����ʽ�Ӳ�������
����ʽ�Ӳ�������
����![]() ʱ��
ʱ��![]() �ɻ�Ϊ��
�ɻ�Ϊ��![]() ����ã�
����ã�![]() ��
��
����������![]() ��
��![]() ��
��
��4���������֪����A��ʾ����Ϊ��-1������B��ʾ�����ǡ�9����������֪�ɵã�
![]() ��
��![]() ����P��Q���1����λ����ʱ��Ҫ�ֵ�Q�ڵ�P�ұߺ͵�Q�ڵ�P������������������
����P��Q���1����λ����ʱ��Ҫ�ֵ�Q�ڵ�P�ұߺ͵�Q�ڵ�P������������������
����ͼ1����Q��P���ұ�ʱ����![]() �ɵ���
�ɵ���![]() ����
����![]() ����ã�
����ã�![]() ��
��
����ͼ2����Q��P�����ʱ����![]() �ɵã�
�ɵã�![]() ����
����![]() �����
�����![]() ��
��
����������![]() ��
��![]() .
.


 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABCD�У�EΪ��CD���е㣬����AE���ӳ�������BC���ӳ����ڵ�F��
��1����֤���ı���ACFD��ƽ���ı��Σ�
��2�������B+��AFB=90�㣬��֤���ı���ACFD�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijЬ���Ⱥ�����7˫ijƷ�Ƶ��˶�Ь�����������Ϊ(��λ:��):40��39��40��41��42��41��41�����������ݵ�������( )
A. 39 B. 40 C. 41 D. 42
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ͷ��һö��ͨ������������40�Σ���֪�����������Ĵ�����15����������ż���Ĵ����ǣ� ��
A.25B.40C.15D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ���У�����Գ�ͼ�ε��������ĶԳ�ͼ�ε��ǣ� ��
A.�ȱ�������
B.ƽ���ı���
C.����
D.Բ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�AB=12��CD=6���߶�CD��ֱ��AB���˶���A��B����࣬C��D����ࣩ��
��1����D����B���غ�ʱ��AC=_________��
��2����P���߶�AB�ӳ���������һ�㣬�ڣ�1���������£���PA+PB�C2PC��ֵ��
��3��M��N�ֱ���AC��BD���е㣬��BC=4ʱ����MN�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦ���н����ִ�¥���£�����һ¥������Ҫȥ��ͬ¥������������������Լ���˵�������һ¥����+1������һ¥������1����ô����ʦ���¹����е�������¥�����μ�¼���£�+6����3��+9����5����7������λ���㣩
��1����˵������ʦ�Ƿ���ʮ��¥����������
��2����˵������ʦ����Ƿ�ص�������һ¥��
��3���ô�¥ÿ���3m������ÿ���ϻ�����1m��Լ��Ҫ�ĵ�0.01�ȣ��������㣬�������е�����Ҫ�ĵ���ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016����������23��)
������ij��ҵ������Ӧ���������·�չ���ĺ��٣��з���һ���²�Ʒ����֪�з����������ֲ�Ʒ�ijɱ�Ϊ30Ԫ����������������y(���)�����ۼ�x(Ԫ����)�ĺ�������ʽΪ��
![]()
(1)����ҵ���۸ò�Ʒ����������ΪW(��Ԫ)����ֱ��д��������W(��Ԫ)�����ۼ�(Ԫ/��)�ĺ�������ʽ��
(2)���ò�Ʒ���ۼ�x(Ԫ/��)Ϊ����ʱ����ҵ���۸ò�Ʒ��õ����������?����������Ƕ���?
(3)����ҵ���۸ò�Ʒ��������������750��Ԫ����ȷ���ò�Ʒ���ۼ�x(Ԫ/��)��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com