
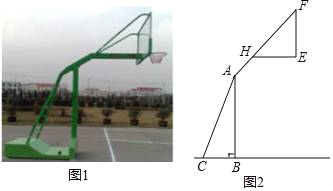
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长![]() 米,HF长
米,HF长![]() 米,HE长1米.
米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
【答案】(1) 篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;(2) 篮板底部点E到地面的距离是(![]() +
+![]() )米
)米
【解析】
(1)由cos∠FHE![]() 可得答案;
可得答案;
(2)延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,据此知GM=AB,HN=EG,Rt△ABC中,求得AB=BCtan60°![]() ;Rt△ANH中,求得HN=AHsin45°
;Rt△ANH中,求得HN=AHsin45°![]() ;根据EM=EG+GM可得答案.
;根据EM=EG+GM可得答案.
(1)在Rt△EFH中,cos∠FHE![]() ,∴∠FHE=45°.
,∴∠FHE=45°.
答:篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;
(2)延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,则四边形ABMG和四边形HNGE是矩形,∴GM=AB,HN=EG.在Rt△ABC中,∵tan∠ACB![]() ,∴AB=BCtan60°=1
,∴AB=BCtan60°=1![]() ,∴GM=AB
,∴GM=AB![]() .在Rt△ANH中,∠FAN=∠FHE=45°,∴HN=AHsin45°
.在Rt△ANH中,∠FAN=∠FHE=45°,∴HN=AHsin45°![]() ,∴EM=EG+GM
,∴EM=EG+GM![]() .
.
答:篮板底部点E到地面的距离是(![]() )米.
)米.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③![]() =
=![]() ;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )

A. ①② B. ①②③ C. ①④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
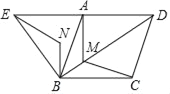
【题目】如图,四边形ABCD是菱形,AB=4,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1═![]() (x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
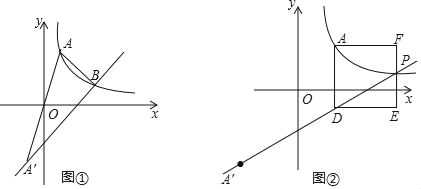
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m=![]() ,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
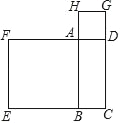
【题目】如图,矩形ABCD的周长是20cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为68cm2,那么矩形ABCD的面积是( )
A. 9cm2 B. 16cm2 C. 21cm2 D. 24cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究:
有A,B两个不透明的布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字-1,-2和-3.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点![]() 的一个坐标为
的一个坐标为![]() .
.
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
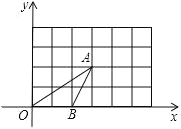
【题目】如图,△OAB的顶点坐标分别为O(0,0)、A(3,2)、B(2,0),将这三个顶点的坐标同时扩大到原来的2倍,得到对应点D、E、F.
(1)在图中画出△DEF;
(2)点E是否在直线OA上?为什么?
(3)△OAB与△DEF______位似图形(填“是”或“不是”)
查看答案和解析>>
科目:初中数学 来源: 题型:
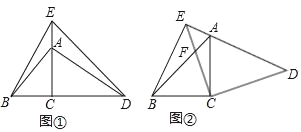
【题目】已知△ABC和△CDE都为等腰直角三角形,∠ACB=∠ECD=90°.
探究:如图①,当点A在边EC上,点C在线段BD上时,连结BE、AD.求证:BE=AD,BE⊥AD.
拓展:如图②,当点A在边DE上时,AB、CE交于点F,连结BE.若AE=2,AD=4,则![]() 的值为 .
的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com