
分析 先整理得2(m2-2m)2-(m2-2m)-1=0,利用因式分解法把原方程化为2(m2-2m)+1=0或(m2-2m)-1=0,然后利用配方法分别解两个一元二次方程即可.
解答 解:2(m2-2m)2-(m2-2m)-1=0,
[2(m2-2m)+1][(m2-2m)-1]=0,
2(m2-2m)+1=0或(m2-2m)-1=0,
解方程2(m2-2m)+1=0得m1=1+$\frac{\sqrt{2}}{2}$,m2=1-$\frac{\sqrt{2}}{2}$,
解方程(m2-2m)-1=0得m1=1+$\sqrt{2}$,m2=1-$\sqrt{2}$,
所以m1=1+$\frac{\sqrt{2}}{2}$,m2=1-$\frac{\sqrt{2}}{2}$,m3=1+$\sqrt{2}$,m4=1-$\sqrt{2}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
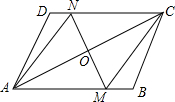 如图,在?ABCD中,点O是对角线AC的中点,过点O的直线MN分别交AB、CD于点M、N,连结AN,CM.
如图,在?ABCD中,点O是对角线AC的中点,过点O的直线MN分别交AB、CD于点M、N,连结AN,CM.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
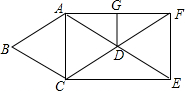 如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF,则下列描述正确的是( )
如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF,则下列描述正确的是( )| A. | 四边形ACEF是平行四边形,它的周长是4 | |
| B. | 四边形ACEF是矩形,它的周长是2+2$\sqrt{3}$ | |
| C. | 四边形ACEF是平行四边形,它的周长是4$\sqrt{3}$ | |
| D. | 四边形ACEF是矩形,它的周长是4+4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
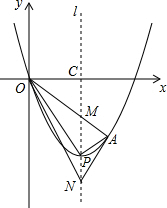 如图,顶点为P(2,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,
如图,顶点为P(2,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
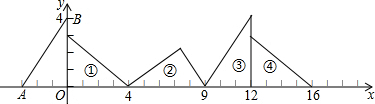
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20 | B. | 19.5 | C. | 14.5 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com