
����Ŀ��ij��˾�ƻ�Ͷ��![]() ��
��![]() ���ֲ�Ʒ����ֻͶ��
���ֲ�Ʒ����ֻͶ��![]() ��Ʒ�����������
��Ʒ�����������![]() ����Ԫ����Ͷ�ʽ��
����Ԫ����Ͷ�ʽ��![]() ����Ԫ��֮��Ĺ�ϵ��ͼ��ʾ����ֻͶ��
����Ԫ��֮��Ĺ�ϵ��ͼ��ʾ����ֻͶ��![]() ��Ʒ�����������
��Ʒ�����������![]() ����Ԫ����Ͷ�ʽ��
����Ԫ����Ͷ�ʽ��![]() ����Ԫ���ĺ�����ϵʽΪ
����Ԫ���ĺ�����ϵʽΪ![]() ��
��
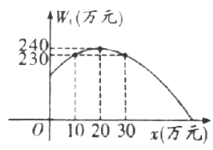
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2����Ͷ��![]() ��Ʒ�������������ֵ��Ͷ��
��Ʒ�������������ֵ��Ͷ��![]() ��Ʒ�������������ֵ��
��Ʒ�������������ֵ��![]() ��Ԫ����
��Ԫ����![]() ��ֵ��
��ֵ��
��3���ù�˾�O![]() ��Ԫ�ʽ�ͬʱͶ��
��Ԫ�ʽ�ͬʱͶ��![]() ��
��![]() ���ֲ�Ʒ����Ͷ��
���ֲ�Ʒ����Ͷ��![]() ��Ʒ���ʽ�Ϊ
��Ʒ���ʽ�Ϊ![]() ��Ԫ������õ����������
��Ԫ������õ����������![]() ��Ԫ����
��Ԫ����![]() ʱ��
ʱ��![]() ��
��![]() ����������٣���
����������٣���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]()
��������
��1����ͼ��ɵú��������ߵĶ������꼰�����ĵ㣬�ɴ���ϵ����������⣻
��2���ɣ�1���ɵ�![]() �����ֵ����
�����ֵ����![]() �ĺ�������ʽ���
�ĺ�������ʽ���![]() ��Ʒ�������������ֵ�������������з�����⼴�ɣ�
��Ʒ�������������ֵ�������������з�����⼴�ɣ�
��3����![]() ��
��![]() �����������ɶ��κ������ʿɵ������߶Գ�����30����ߣ��ɴ˵ù���n�IJ���ʽ��⼴�ɣ�
�����������ɶ��κ������ʿɵ������߶Գ�����30����ߣ��ɴ˵ù���n�IJ���ʽ��⼴�ɣ�
�⣺��1����ͼ���֪��![]() �������ߵĶ������꣬
�������ߵĶ������꣬
��![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]() ��
��
��![]() ��
��![]() ��������
��������![]() �ϣ�
�ϣ�
![]() ��
��
���![]() ��
��
![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]() ��
��
��2���ɣ�1���ã�Ͷ��![]() ��Ʒ�������������ֵΪ
��Ʒ�������������ֵΪ![]() ��
��
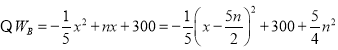 ��
��
![]() Ͷ��
Ͷ��![]() ��Ʒ�������������ֵΪ
��Ʒ�������������ֵΪ![]() ��
��
������ɵã�![]() �����
�����![]() ��
��
![]() ��
��![]() ʱ���������⣬
ʱ���������⣬
![]() ��
��
��3��������ɵã�![]() ��
��
![]()
![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
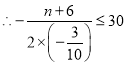
���![]() ��
��
![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]() ��
��


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�е�����A(1��0)��B(��1��0)��P(0����1)�����߶�AB��y������ƽ��m(m��0)����λ���ȣ��õ��߶�CD�����κ���y��a(x��h)2��k��ͼ����P��C��D��
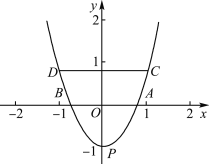
(1)��m��1ʱ��a��______����m��2ʱ��a��______��
(2)����a��m�Ĺ�ϵ����֤����IJ��룻
(3)���߶�AB��y������ƽ��n(n��0)����λ���ȣ��õ��߶�C1D1����C1��D1�ֱ����A��B��Ӧ�����κ���y��2a(x��h)2��k��ͼ����P��C1��D1��
����n��m֮��Ĺ�ϵ��
�ڵ���COD1��ֱ��������ʱ��ֱ��д��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
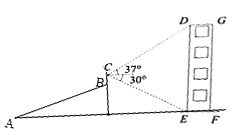
����Ŀ��ijͬѧ������ѧ֪ʶ����������DEFG�ĸ߶ȣ����ӵ�![]() ���������¶�Ϊ
���������¶�Ϊ![]() ��б��AB����26�����B�����ò���Dz�ý����ﶥ��
��б��AB����26�����B�����ò���Dz�ý����ﶥ��![]() ������Ϊ37�㣬�������
������Ϊ37�㣬�������![]() �ĸ���Ϊ30�㣬��AFΪˮƽ�ĵ��棬�������ֱ���ã���߶�BC=1.6�ף���˽�����ĸ߶�DEԼΪ(��ȷ��
�ĸ���Ϊ30�㣬��AFΪˮƽ�ĵ��棬�������ֱ���ã���߶�BC=1.6�ף���˽�����ĸ߶�DEԼΪ(��ȷ��![]() �ף��ο����ݣ�
�ף��ο����ݣ�![]() ��
��![]() )�� ��
)�� ��
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
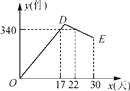
����Ŀ��ij��˾������һ���µĽ��ܲ�Ʒ���ò�Ʒ�ijɱ���Ϊ6Ԫ/�����ò�Ʒ����ʽͶ���г�ǰͨ�������������Ϊ��һ����(30��)�������ۣ��ۼ�Ϊ8Ԫ/����������Ա��������������˸��ټ�¼��������¼������ͼ��(��ͼ)��ͼ�е�����ODE��ʾ��������y(��)������ʱ��x(��)֮��ĺ�����ϵ����֪�߶�DE��ʾ�ĺ�����ϵ�У�ʱ��ÿ����1�죬������������5����
(1)��24������������� ���������������� Ԫ��
(2)��y��x֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ��
(3)������������640Ԫ���������ж����죿�������ڼ䣬��������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����һ������������������������ת![]() ������ͼ����ԭͼ���ص��������������Σ���ͼ2����һ����������������������ת 45��������ͼ����ԭͼ�ε��ص����������˱��Σ����˹��ɣ���һ�����߱�����������������ת______
������ͼ����ԭͼ���ص��������������Σ���ͼ2����һ����������������������ת 45��������ͼ����ԭͼ�ε��ص����������˱��Σ����˹��ɣ���һ�����߱�����������������ת______![]() ������ͼ����ԭͼ���ص�������������Σ���ͼ2�У��������εı߳�Ϊ
������ͼ����ԭͼ���ص�������������Σ���ͼ2�У��������εı߳�Ϊ![]() �����������˱��ε����Ϊ_______��
�����������˱��ε����Ϊ_______��


ͼ1 ͼ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
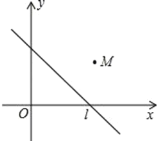
����Ŀ����ͼ����֪�� M ������Ϊ��4��3������ M ����ֱ�� l��y����x+b �ĶԳƵ������������ϣ��� b��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
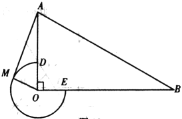
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ���Ե�
���Ե�![]() ΪԲ�ģ���
ΪԲ�ģ���![]() Ϊ�뾶���Ż�
Ϊ�뾶���Ż�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() .��
.��![]() ���Ż�
���Ż�![]() �ϴӵ�
�ϴӵ�![]() ��ʼ�ƶ��������
��ʼ�ƶ��������![]() ʱֹͣ������
ʱֹͣ������![]() .
.
��1����![]() ʱ���ж�
ʱ���ж�![]() ���Ż�
���Ż�![]() ��λ�ù�ϵ��������֤����
��λ�ù�ϵ��������֤����
��2����![]() ʱ�����
ʱ�����![]() ���Ż�
���Ż�![]() ���ƶ���·�߳����߶�
���ƶ���·�߳����߶�![]() �ij�.
�ij�.
��3������![]() ����
����![]() �����Ϊ
�����Ϊ![]() ��ֱ��д��
��ֱ��д��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.

����ͼ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ר��������A��B�����ͺŵ�����Դ�����������۳�1��A�ͳ���3��B�ͳ������ֳ��͵������ܶ�Ϊ96��Ԫ����������2��A�ͳ���1��B�ͳ������ֳ��͵������ܶ�Ϊ62��Ԫ����֪�����ͺ��������ۼ۸�ʼ�ղ��䣮
��1����A��B���ֳ��͵����۵��۷ֱ��Ƕ��٣�
��2�������ܼƻ��۳�A��B�����ͺŵij���5�����������ܶ����100��Ԫ����B�ͳ�����Ҫ�۳���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
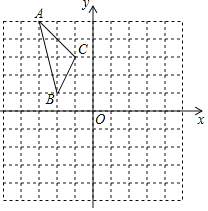
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA����3��5����B����2��1����C����1��3����
��1������ABC����ƽ�ƺ�õ���A1B1C1����֪��C�Ķ�Ӧ��C������Ϊ��4����1����������A1B1C1��д������A��B��Ӧ��A1��B1�����ꣻ
��2������ABC���ŵ�O��˳ʱ�뷽����ת90��õ���A2B2C2��������A2B2C2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com