
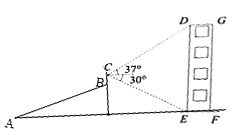
【题目】某同学利用数学知识测量建筑物DEFG的高度.他从点![]() 出发沿着坡度为
出发沿着坡度为![]() 的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端
的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端![]() 的仰角为37°,建筑物底端
的仰角为37°,建筑物底端![]() 的俯角为30°,若AF为水平的地面,侧角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到
的俯角为30°,若AF为水平的地面,侧角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到![]() 米,参考数据:
米,参考数据:![]() ,
,![]() )( )
)( )
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
【答案】C
【解析】
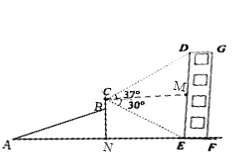
如图,设CB⊥AF于N,过点C作CM⊥DE于M,根据坡度及AB的长可求出BN的长,进而可求出CN的长,即可得出ME的长,利用∠MBE的正切可求出CM的长,利用∠DCM的正切可求出DM的长,根据DE=DM+ME即可得答案.
如图,设CB⊥AF于N,过点C作CM⊥DE于M,
∵沿着坡度为![]() 的斜坡AB步行26米到达点B处,
的斜坡AB步行26米到达点B处,
∴![]() ,
,
∴AN=2.4BN,
∴BN2+(2.4BN)2=262,
解得:BN=10(负值舍去),
∴CN=BN+BC=11.6,
∴ME=11.6,
∵∠MCE=30°,
∴CM=![]() =11.6
=11.6![]() ,
,
∵∠DCM=37°,
∴DM=CM·tan37°=8.7![]() ,
,
∴DE=ME+DM=11.6+8.7![]() ≈26.7(米),
≈26.7(米),
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知A![]() ,B
,B![]() 是一次函数y=kx+b与反比例函数
是一次函数y=kx+b与反比例函数![]() 图象的两个交点.
图象的两个交点.

(1) 根据图象回答:当x满足 ,一次函数的值小于反比例函数的值;
(2) 将直线AB沿y轴方向,向下平移n个单位,与双曲线![]() 有唯一的公共点时,求n的值;
有唯一的公共点时,求n的值;
(3) 如图2,P点在![]() 的图象上,矩形OCPD的两边OD、OC在坐标轴上,且OC=2OD,M、N分别为OC、OD的中点,PN与DM交于点E,直接写出四边形EMON的面积为 .
的图象上,矩形OCPD的两边OD、OC在坐标轴上,且OC=2OD,M、N分别为OC、OD的中点,PN与DM交于点E,直接写出四边形EMON的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学所在年级的500名学生参加志愿者活动,现有以下5个志愿服务项目:A,纪念馆志讲解员.B.书香社区图书整理C.学编中国结及义卖.D,家风讲解员E.校内志愿服务,要求:每位学生都从中选择一个项目参加,为了了解同学们选择这个5个项目的情况,该同学随机对年级中的40名同学选择的志愿服务项目进行了调查,过程如下:
收集数据:设计调查问卷,收集到如下数据(志愿服务项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B,
A,C,E,D,B,A,B,E,C,A,
D,D,B,B,C,C,A,E,B
C,B,D,C,A,C,C,A,C,E,
(1)整理、描述诗句:划记、整理、描述样本数据,绘制统计图如下,请补全统计表和统计图

选择各志愿服务项目的人数统计表
志愿服务项目 | 划记 | 人数 |
A.纪念馆志愿讲解员 | 正 | 8 |
B.书香社区图书整理 | ||
C.学编中国结及义卖 | 正正 | 12 |
D.家风讲解员 | ||
E.校内志愿服务 | 正 一 | 6 |
合计 | 40 | 40 |
分析数据、推断结论
(2)抽样的40个样本数据(志愿服务项目的编号)的众数是 (填A﹣E的字母代号)
(3)请你任选A﹣E中的两个志愿服务项目,根据该同学的样本数据估计全年级大约有多少名同学选择这两个志愿服务项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《小猪佩奇》这部动画片,估计同学们都非常喜欢.周末,小猪佩奇一家4口人(小猪佩奇,小猪乔治,小猪妈妈,小猪爸爸)到一家餐厅就餐,包厢有一圆桌,旁边有四个座位(![]() ,
,![]() ,
,![]() ,
,![]() ).
).


(1)小猪佩奇随机坐到![]() 座位的概率是________;
座位的概率是________;
(2)若现在由小猪佩奇,小猪乔治两人先后选座位,用树状图或列表的方法计算出小猪佩奇和小猪乔治坐对面的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,∠C=90°,O是斜边AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与BC交于点F,与AC相切于点D,连接DF、BD,且BD平分∠ODF.
中,∠C=90°,O是斜边AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与BC交于点F,与AC相切于点D,连接DF、BD,且BD平分∠ODF.
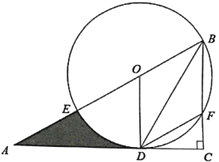
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,求阴影部分的面积(结果保留
,求阴影部分的面积(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 的直径
的直径![]() ,点
,点![]() 是
是![]() 延长线上的一点,过
延长线上的一点,过![]() 点作
点作![]() 的切线,切点为
的切线,切点为![]() ,连接
,连接![]() .
.

(1)若![]() ,求
,求![]() 的长;
的长;
(2)若点![]() 在
在![]() 的延长线上运动,
的延长线上运动,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,你认为
,你认为![]() 的大小是否发生变化?若变化,请说明理由;若不变化,求出
的大小是否发生变化?若变化,请说明理由;若不变化,求出![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
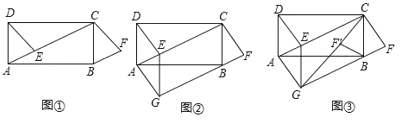
【题目】(操作)如图①,在矩形![]() 中,
中,![]() 为对角线
为对角线![]() 上一点(不与点
上一点(不与点![]() 重合),将
重合),将![]() 沿射线
沿射线![]() 方向平移到
方向平移到![]() 的位置,
的位置,![]() 的对应点为
的对应点为![]() .已知
.已知![]() (不需要证明).
(不需要证明).
(探究)过图①中的点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() ,其它条件不变,如图②.求证:
,其它条件不变,如图②.求证:![]() .
.
(拓展)将图②中的![]() 沿
沿![]() 翻折得到
翻折得到![]() ,连接
,连接![]() ,其它条件不变,如图③.当
,其它条件不变,如图③.当![]() 最短时,若
最短时,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长和此时四边形
的长和此时四边形![]() 的周长.
的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com