练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知二次函数．

    （1）写出该二次函数图象的对称轴及顶点坐标，再描点画图；

    （2）利用图象回答：当x取什么值时，．

    【答案】（1）对称轴是：直线x=2，顶点坐标是：（2，-1），图象见详解；（2）1<x<3.

    【解析】

    （1）根据顶点的坐标公式，可得到对称轴方程和顶点坐标，再求出图象与坐标轴的交点坐标，即可画出二次函数的图象；

    （2）根据二次函数的图象，即可求出x的取值范围.

    （1）∵a=1，b=-4，c=3，

    ∴，===-1，

    ∴对称轴是：直线x=2，顶点坐标是：（2，-1）；

    令y=0，则的根是：，令 x=0，y=3，

    ∴二次函数图象与x轴交点坐标：（1，0）（3，0），与y轴交点坐标是：（0，3），

    如图所示：

    （2）由二次函数的图象，可知：当1<x<3时，．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

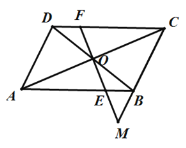
    【题目】如图，ABCD的对角线AC，BD相交于点O，EF经过点O，分别交AB，CD于点E，F，FE的延长线交CB的延长线于点M．

    (1)求证：OE＝OF；

    (2)若AD＝4，AB＝6，BM＝1，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某同学利用数学知识测量建筑物DEFG的高度．他从点出发沿着坡度为的斜坡AB步行26米到达点B处，用测角仪测得建筑物顶端的仰角为37°，建筑物底端的俯角为30°，若AF为水平的地面，侧角仪竖直放置，其高度BC=1.6米，则此建筑物的高度DE约为(精确到米，参考数据：，)（ ）

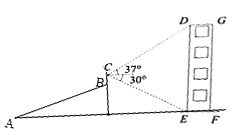
    A.米B.米C.米D.米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠MON及其边上一点A，以点A为圆心，AO长为半径画弧，分别交OM，ON于点B和C，再以点C为圆心，AC长为半径画弧，恰好经过点B，错误的结论是（ ）.

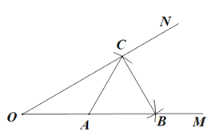
    A.B.∠OCB＝90°C.∠MON＝30°D.OC＝2BC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一科技小组进行了机器人行走性能试验，在试验场地有A、B、C三点顺次在同一笔直的赛道上，甲、乙两机器人分别从A、B两点同时同向出发，历时7min同时到达C点，甲机器人前3分钟以a m/min的速度行走，乙机器人始终以60m/min的速度行走，如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象，请结合图象，回答下列问题：

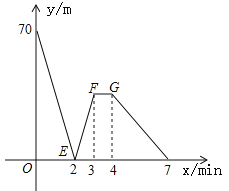
    (1)A、B两点之间的距离是____m，A、C两点之间的距离是____m，a=____m/min；

    (2)求线段EF所在直线的函数解析式；

    (3)设线段FG∥x轴.

    ①当3≤x≤4时，甲机器人的速度为____m/min；

    ②直接写出两机器人出发多长时间相距28m.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面给出六个函数解析式：，，，，，．

    小明根据学习二次函数的经验，分析了上面这些函数解析式的特点，研究了它们的图象和性质。下面是小明的分析和研究过程，请补充完整：

    （1）观察上面这些函数解析式，它们都具有共同的特点，可以表示为形如_______，其中x为自变量；

    （2）如图，在平面直角坐标系中，画出了函数的部分图象，用描点法将这个函数的图象补充完整；

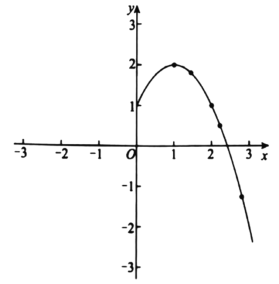
    （3）对于上面这些函数，下列四个结论：

    ①函数图象关于y轴对称

    ②有些函数既有最大值，同时也有最小值

    ③存在某个函数，当（m为正数）时，y随x的增大而增大，当时，y随x的增大而减小

    ④函数图象与x轴公共点的个数只可能是0个或2个或4个

    所有正确结论的序号是________；

    （4）结合函数图象，解决问题：若关于x的方程有一个实数根为3，则该方程其它的实数根为_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

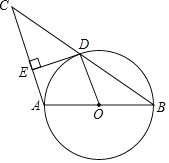
    【题目】如图，以△ABC的边AB为直径的⊙O恰好过BC的中点D，过点D作DE⊥AC于E，连结OD，则下列结论中：①OD∥AC；②∠B＝∠C；③2OA＝BC；④DE是⊙O的切线；⑤∠EDA＝∠B，正确的序号是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=x2+2ax-3与x轴交于A、B(1，0)两点(点A在点B的左侧)，与y轴交于点C，将抛物线沿y轴平移m(m＞0)个单位，当平移后的抛物线与线段OA有且只有一个交点时，则m的取值范围是_______________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

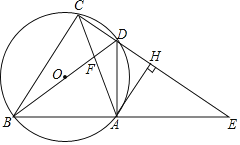
    【题目】如图，四边形ABCD的顶点在⊙O上，BD是⊙O的直径，延长CD、BA交于点E，连接AC、BD交于点F，作AH⊥CE，垂足为点H，已知∠ADE＝∠ACB．

    （1）求证：AH是⊙O的切线；

    （2）若OB＝4，AC＝6，求sin∠ACB的值；

    （3）若，求证：CD＝DH．

    查看答案和解析>>

    同步练习册答案