
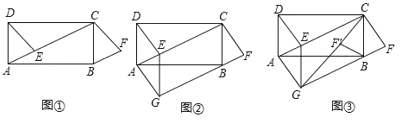
【题目】(操作)如图①,在矩形![]() 中,
中,![]() 为对角线
为对角线![]() 上一点(不与点
上一点(不与点![]() 重合),将
重合),将![]() 沿射线
沿射线![]() 方向平移到
方向平移到![]() 的位置,
的位置,![]() 的对应点为
的对应点为![]() .已知
.已知![]() (不需要证明).
(不需要证明).
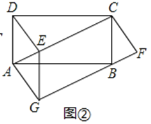
(探究)过图①中的点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() ,其它条件不变,如图②.求证:
,其它条件不变,如图②.求证:![]() .
.
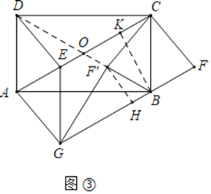
(拓展)将图②中的![]() 沿
沿![]() 翻折得到
翻折得到![]() ,连接
,连接![]() ,其它条件不变,如图③.当
,其它条件不变,如图③.当![]() 最短时,若
最短时,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长和此时四边形
的长和此时四边形![]() 的周长.
的周长.
【答案】探究:见解析;拓展:![]() 四边形
四边形![]() 的周长为
的周长为![]()
【解析】
探究:证明四边形EGBC是平行四边形,推出EG=BC,利用SAS证明三角形全等即可.
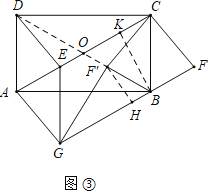
拓展:如图3中,连接BD交AC于点O,作BK⊥AC于K,F′H⊥BC于H.由题意四边形AGFC是平行四边形,推出GF=AC=![]() ,由BF=BF′,可以假设BF=x,则BG=
,由BF=BF′,可以假设BF=x,则BG=![]() 利用相似三角形的性质,求出BH,HF′,利用勾股定理求出GF′,再利用二次函数的性质,求出GF′的值最小时BF′的值,推出BF′=
利用相似三角形的性质,求出BH,HF′,利用勾股定理求出GF′,再利用二次函数的性质,求出GF′的值最小时BF′的值,推出BF′=![]() 此时点F′与O重合,由此即可解决问题.
此时点F′与O重合,由此即可解决问题.
解:探究:由平移![]() ,
,![]()
∴![]() ,即
,即![]()
又∵![]() ,∴四边形
,∴四边形![]() 为平行四边形
为平行四边形
∴![]()
∵![]() ,∴∠CBF=∠ACB,
,∴∠CBF=∠ACB,
∵![]()
∴∠AEG=∠ACB,
∴∠AEG=∠CBF
∴![]() .
.
拓展:
如图3中,连接BD交AC于点O,作BK⊥AC于K,F′H⊥BC于H.
∵四边形ABCD是矩形, ∴∠ABC=90°,AB=4,BC=2,
∴![]()
∵![]()
∴![]() ,
,
∴![]()
由题意四边形AGFC是平行四边形, ∴GF=AC=![]() ,
,
∵BF=BF′,可以假设BF=x,则BG=![]()
∵AC∥GF, ∴∠BOK=∠HBF′,
∵∠BKO=∠F′HB=90°,
∴△F′HB∽△BKO,
∴ ![]()
∴ 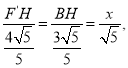
∴![]()
∴![]()
∵ ![]() >0,
>0,
∴当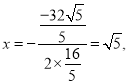 时,GF′的值最小,
时,GF′的值最小,
此时点F′与O重合,由对折得:![]()
由矩形的性质得:![]()
![]()
![]() 四边形BFCF′是菱形,
四边形BFCF′是菱形,
![]() 四边形BFCF′的周长为
四边形BFCF′的周长为![]() ,
,
![]() 且
且![]() 与
与![]() 互相平分,
互相平分,
由勾股定理得:![]()


科目:初中数学 来源: 题型:
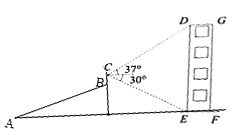
【题目】某同学利用数学知识测量建筑物DEFG的高度.他从点![]() 出发沿着坡度为
出发沿着坡度为![]() 的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端
的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端![]() 的仰角为37°,建筑物底端
的仰角为37°,建筑物底端![]() 的俯角为30°,若AF为水平的地面,侧角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到
的俯角为30°,若AF为水平的地面,侧角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到![]() 米,参考数据:
米,参考数据:![]() ,
,![]() )( )
)( )
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
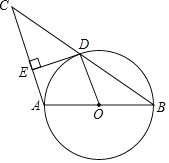
【题目】如图,以△ABC的边AB为直径的⊙O恰好过BC的中点D,过点D作DE⊥AC于E,连结OD,则下列结论中:①OD∥AC;②∠B=∠C;③2OA=BC;④DE是⊙O的切线;⑤∠EDA=∠B,正确的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+2ax-3与x轴交于A、B(1,0)两点(点A在点B的左侧),与y轴交于点C,将抛物线沿y轴平移m(m>0)个单位,当平移后的抛物线与线段OA有且只有一个交点时,则m的取值范围是_______________
查看答案和解析>>
科目:初中数学 来源: 题型:
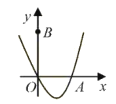
【题目】如图,在平面直角坐标系中,![]() 为坐标原点.抛物线
为坐标原点.抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 是该抛物线第一象限图像上的一点,
是该抛物线第一象限图像上的一点,![]() 三点均在某一个正方形的边上,且该正方形的任何一条边均与某条坐标轴平行,设点
三点均在某一个正方形的边上,且该正方形的任何一条边均与某条坐标轴平行,设点![]() 的横坐标为
的横坐标为![]() .若这个正方形的面积最小,则
.若这个正方形的面积最小,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校组织“学经典,用经典”知识竞赛,每班参加比赛的学生人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为
四个等级,其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分,
分,![]() 分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
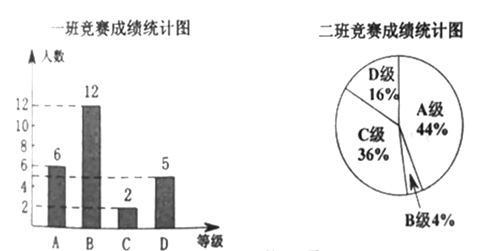
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩“![]() 级”的人数为 ;
级”的人数为 ;
(2)请你将下表补充完整:
平均数(分) | 中位数(分) | 众数(分) | |
一班 |
|
| |
二班 |
|
|
(3)请你对这次两班成绩统计数据的结果进行分析(写出一条结论即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地计划对![]() 、
、![]() 两类薄弱学校全部进行改造:根据预算,共需资金1575万元,已知改造一所
两类薄弱学校全部进行改造:根据预算,共需资金1575万元,已知改造一所![]() 类学校和两所
类学校和两所![]() 类学校共需资金230万元;改造两所
类学校共需资金230万元;改造两所![]() 类学校和一所
类学校和一所![]() 类学校共需资金205万元,
类学校共需资金205万元,
(1)求改造一所![]() 类学校和一所
类学校和一所![]() 类学校所需的资金分别是多少万元?
类学校所需的资金分别是多少万元?
(2)若该地的![]() 类学校不超过5所,则
类学校不超过5所,则![]() 类学校至少有多少所?
类学校至少有多少所?
查看答案和解析>>
科目:初中数学 来源: 题型:
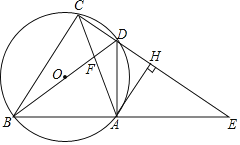
【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若![]() ,求证:CD=DH.
,求证:CD=DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com