
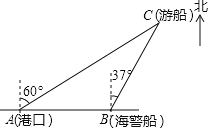
【题目】一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,
(1)求点C到直线AB的距离;
(2)求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
科目:初中数学 来源: 题型:
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上一点O为圆心,OB为半径作⊙O,交AC于点E,交AB于点D,且∠BEC=∠BDE.

(1)求证:AC是⊙O的切线;
(2)连接OC交BE于点F,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,数据整理过程如下,请完成下面数据整理中的问题:
(1)收集数据
从甲、乙两个班中各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班:65,75,75,80,60,50,75,90,85,65;
乙班:90,55,80,70,55,70,95,80,65,70;
(2)整理描述数据
按如下分数段整理、描述这两组样本数据:
成绩x 人数 班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m= ,n= ;
(3)分析数据
①若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有 人;
②现从甲班指定的3名学生(1男2女),乙班指定的2名学生(1男1女)中分别抽取1名学生去参加身体素质拓展训练,用树状图或列表法求出抽到的2名同学中恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.
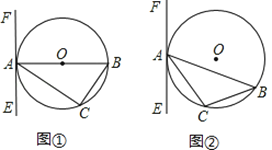
(1)如图①所示,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(至少说出两种): 或者 .
(2)如图②所示,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
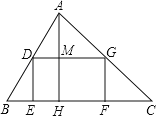
【题目】如图,有一块三角形的土地,它的一条边BC=100米,DC边上的高AH=80米,某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分別在边AB、AC上.若大楼的宽是40米(即DE=40米),则这个矩形的面积是_____平方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顶点为D的抛物线y=﹣x2+bx+c交x轴于A、B(3,0),交y轴于点C,直线y=﹣![]() x+m经过点C,交x轴于E(4,0).
x+m经过点C,交x轴于E(4,0).
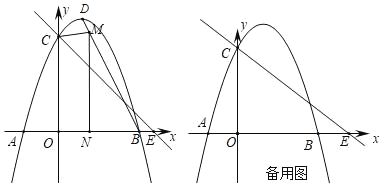
(1)求出抛物线的解析式;
(2)如图1,点M为线段BD上不与B、D重合的一个动点,过点M作x轴的垂线,垂足为N,设点M的横坐标为x,四边形OCMN的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点P为x轴的正半轴上一个动点,过P作x轴的垂线,交直线y=﹣![]() x+m于G,交抛物线于H,连接CH,将△CGH沿CH翻折,若点G的对应点F恰好落在y轴上时,请直接写出点P的坐标.
x+m于G,交抛物线于H,连接CH,将△CGH沿CH翻折,若点G的对应点F恰好落在y轴上时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,AM,BN 分别是⊙O 的切线,切点分别为 P,M,N.若 MN∥AB,∠A=60°,AB=6,则⊙O 的半径是( )
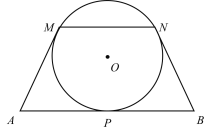
A.![]() B.3C.
B.3C.![]()
![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com