
����Ŀ������ΪD��������y����x2+bx+c��x����A��B(3��0)����y���ڵ�C��ֱ��y����![]() x+m������C����x����E(4��0)��
x+m������C����x����E(4��0)��
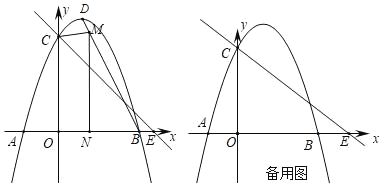
(1)��������ߵĽ���ʽ��
(2)��ͼ1����MΪ�߶�BD�ϲ���B��D�غϵ�һ�����㣬����M��x��Ĵ��ߣ�����ΪN�����M�ĺ�����Ϊx���ı���OCMN�����ΪS����S��x֮��ĺ�����ϵʽ������S�����ֵ��
(3)��PΪx�����������һ�����㣬��P��x��Ĵ��ߣ���ֱ��y����![]() x+m��G������������H������CH������CGH��CH���ۣ�����G�Ķ�Ӧ��Fǡ������y����ʱ����ֱ��д����P�����꣮
x+m��G������������H������CH������CGH��CH���ۣ�����G�Ķ�Ӧ��Fǡ������y����ʱ����ֱ��д����P�����꣮
���𰸡�(1)y����x2+2x+3��(2)S����(x��![]() )2+
)2+![]() ����x��
����x��![]() ʱ��S�����ֵ�����ֵΪ
ʱ��S�����ֵ�����ֵΪ![]() ��(3)���ڣ���P������Ϊ(4��0)��(
��(3)���ڣ���P������Ϊ(4��0)��(![]() ��0).
��0).
��������
��1������E����ֱ�߽���ʽ�У��������C�����꣬����C��B���������߽���ʽ�У�����������߽���ʽ��
��2���������߽���ʽ��ɶ���ʽ���������D�����꣬��ֱ��BD�Ľ���ʽ�������B��D�������ֱ��BD�Ľ���ʽ����MN�ɱ�ʾ����S�ɱ�ʾ��
��3�����P�����꣬���G������ɱ�ʾ����H������ɱ�ʾ��HG���ȿɱ�ʾ�����÷����Ƴ�CG��HG���е�ʽ��⼴�ɣ�
��1������E����ֱ�߽���ʽ�У�
0����![]() ��4+m��
��4+m��
���m��3��
�����ʽΪy����![]() x+3��
x+3��
��C(0��3)��
��B(3��0)��
����![]() ��
��
���![]() ��
��
�������ߵĽ���ʽΪ��y����x2+2x+3��
��2����y����x2+2x+3����(x��1)2+4��
��D(1��4)��
��ֱ��BD�Ľ���ʽΪy��kx+b�������B��D��
![]() ��
��
���![]() ��
��
��ֱ��BD�Ľ���ʽΪy����2x+6��
���M������Ϊ(x����2x+6)��
��S��(3+6��2x)x![]() ����(x��
����(x��![]() )2+
)2+![]() ��
��
�൱x��![]() ʱ��S�����ֵ�����ֵΪ
ʱ��S�����ֵ�����ֵΪ![]() ��
��
(3)���ڣ�
��ͼ��ʾ��
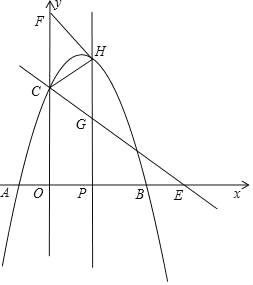
���P������Ϊ(t��0)��
���G(t����![]() t+3)��H(t����t2+2t+3)��
t+3)��H(t����t2+2t+3)��
��HG��|��t2+2t+3��(��![]() t+3)|��|t2��
t+3)|��|t2��![]() t|
t|
CG��![]() ��
��![]() t��
t��
�ߡ�CGH��GH���ۣ�G�Ķ�Ӧ��Ϊ��F��F����y���ϣ�
��HG��y�ᣬ
��HG��CF��HG��HF��CG��CF��
��GHC����CHF��
���FCH����CHG��
���FCH����FHC��
���GCH����GHC��
��CG��HG��
��|t2��![]() t|��
t|��![]() t��
t��
��t2��![]() t��
t��![]() tʱ��
tʱ��
���t1��0(��)��t2��4��
��ʱ��P(4��0)��
��t2��![]() t����
t����![]() tʱ��
tʱ��
���t1��0(��)��t2��![]() ��
��
��ʱ��P(![]() ��0)��
��0)��
���ϣ���P������Ϊ(4��0)��(![]() ��0)��
��0)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
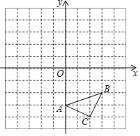
����Ŀ����ͼ���������������У�ÿ��С�����εı߳���![]() ����λ���ȣ��Ե�
����λ���ȣ��Ե�![]() Ϊλ�����ģ��������л�
Ϊλ�����ģ��������л�![]() ��ʹ
��ʹ![]() ��
��![]() λ�ƣ���
λ�ƣ���![]() ��
��![]() ��λ�Ʊ�Ϊ
��λ�Ʊ�Ϊ![]() �����
�����![]() ����������� ��
����������� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
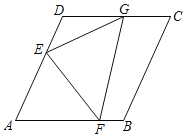
����Ŀ����ͼ������ֽƬABCD�У�AB��4����B��120����������ֽƬ���ۣ�ʹ��A���ڱ�CD���е�G�����ۺ�ΪEF����E��F�ֱ��ڱ�AD��AB�ϣ���sin��GEF��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
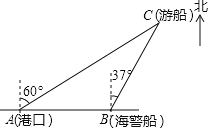
����Ŀ��һ�ҹ۹��δ��Ӹۿ�A�Ա�ƫ��60��ķ�����۹۹⣬����80������C��ʱ�����˲෭�����¹ʣ���������������źţ�һ���ڸۿ���������ĺ������ӵ�����źţ�����¹ʴ������ı�ƫ��37�㷽��������40����ÿСʱ���ٶ�ǰ����Ԯ��
��1�����C��ֱ��AB�ľ��룻
��2�����������¹ʴ�C������Ĵ�Լʱ�䣮����ܰ��ʾ��sin53���0.8��cos53���0.6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ʽ��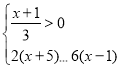
��1�����������ʽ�飬�������������ϱ�ʾ������
��2������x�ķ�ʽ����![]() �Ľ��Dz����������ʽ��������⣿
�Ľ��Dz����������ʽ��������⣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
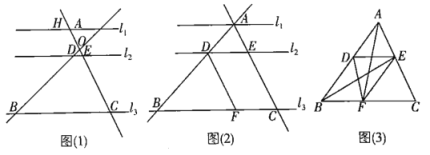
����Ŀ����ͼ(1)��![]() ��ֱ��AB��CH���ڵ�O���ֱ�
��ֱ��AB��CH���ڵ�O���ֱ�![]() ��D��E���㣬��֪
��D��E���㣬��֪![]() ��
��![]() ��
��![]() .
.
(1)����̽������ͼ(1)�У���DB��AD�ij���
(2)������죺ƽ��ABʹ��A��H�غϣ���ͼ(2)��ʾ������D��![]() ����
����![]() �����߶�BF�ij���
�����߶�BF�ij���
(3)��չǨ�ƣ���ͼ(3)����![]() �������10����D��E�ֱ�λ��AB��CA�ϣ�
�������10����D��E�ֱ�λ��AB��CA�ϣ�![]() ����F��BC����
����F��BC����![]() ��
��![]() �����
�����![]() ��������ı���FCED�������ȣ��������ȵ����.
��������ı���FCED�������ȣ��������ȵ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ʵ��������������ijУ��֯���꼶ѧ����չ��������������ǰ��������30��ѧ��������������ٴβ���ⲿ��ѧ��������������������ݼ�¼���£�
�ǰ�����ѧ���������ݣ�
![]()
����ѧ���������ݣ�
![]()
����ѧ������Ƶ���ֲ���
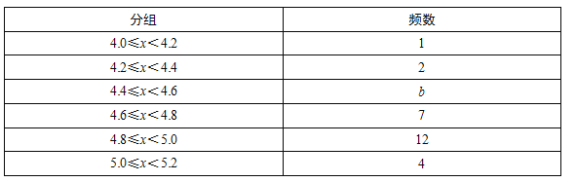
����������Ϣ�ش��������⣺
��1����գ�a=������b=�������ǰ�����ѧ�������������ݵ���λ��������������ѧ�������������ݵ�������������
��2����������4.8������Ϊ��꣬�������꼶600��ѧ������������������ж��٣�
��3�������ǰ��������ݣ���һ����������ѧУ��չ�����������Ч����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��һ�ŵ���ֱ�������ΰ壬
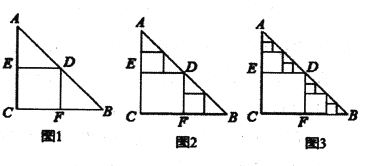
��һ�ŵ���ֱ�������ΰ壬![]() ��Ҫ������ֽ���м�ȡ������(������ͼ1��ʾ)��ͼ1�м�����Ϊ��
��Ҫ������ֽ���м�ȡ������(������ͼ1��ʾ)��ͼ1�м�����Ϊ��![]() �μ�ȡ�������õ����������Ϊ
�μ�ȡ�������õ����������Ϊ![]() ������ͼ1�еļ����������µ�
������ͼ1�еļ����������µ�![]() ��
��![]() �У��ֱ��ȡ����ȫ�������Σ���Ϊ��
�У��ֱ��ȡ����ȫ�������Σ���Ϊ��![]() �μ�ȡ�����������������������Ϊ
�μ�ȡ�����������������������Ϊ![]() ��(��ͼ2) ���������µ��ĸ��������У���ͬ���ķ����ֱ��ȡ�����Σ��õ��ĸ���ͬ�������Σ���Ϊ��
��(��ͼ2) ���������µ��ĸ��������У���ͬ���ķ����ֱ��ȡ�����Σ��õ��ĸ���ͬ�������Σ���Ϊ��![]() �μ�ȡ���������ĸ������ε������Ϊ
�μ�ȡ���������ĸ������ε������Ϊ![]() ��(��ͼ3)������������ȥ���������
��(��ͼ3)������������ȥ���������![]() �μ�ȡ��
�μ�ȡ��![]() ___________��
___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ�ؼҿ�������������������ǰְ��������ͽ����������![]() ����ǰű����ޣ�
����ǰű����ޣ�![]() ��
��![]() ����������ܶԻ�������.��Щ��������һ���İ�װ��װ�ţ����������������.
����������ܶԻ�������.��Щ��������һ���İ�װ��װ�ţ����������������.
��1����������ش�����ȡ��һ�������ȡ�����ǰű����ĸ����Ƕ��٣�
��2��������״ͼ���б�����ʾ��������ش�����ȡ��������������п��ܽ��������ȡ������������������ܶԻ������˵ĸ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com