
ΓΨΧβΡΩΓΩΜΕΜΕΖ≈―ßΜΊΦ“Ω¥ΒΫΉά…œ”–»ΐΗωάώΑϋΘ§ «Α÷Α÷ΥΆΗχΜΕΜΕΚΆΫψΫψΒΡάώΈοΘ§Τδ÷–![]() άώΑϋ «Α≈±»ΆόΆόΘ§
άώΑϋ «Α≈±»ΆόΆόΘ§![]() ΚΆ
ΚΆ![]() άώΑϋΕΦ «÷«ΡήΕ‘ΜΑΜζΤς»Υ.’β–©άώΑϋ”ΟΆβ±μ“Μ―υΒΡΑϋΉΑΚ–ΉΑΉ≈Θ§Ω¥≤ΜΒΫάοΟφΒΡάώΈο.
άώΑϋΕΦ «÷«ΡήΕ‘ΜΑΜζΤς»Υ.’β–©άώΑϋ”ΟΆβ±μ“Μ―υΒΡΑϋΉΑΚ–ΉΑΉ≈Θ§Ω¥≤ΜΒΫάοΟφΒΡάώΈο.
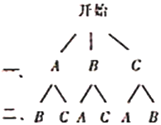
Θ®1Θ©ΜΕΜΕΥφΜζΒΊ¥”Ήά…œ»Γ≥ω“ΜΗωάώΑϋΘ§»Γ≥ωΒΡ «Α≈±»ΆόΆόΒΡΗ≈¬ «Εύ…ΌΘΩ
Θ®2Θ©«κ”Ο ςΉ¥ΆΦΜρΝ–±μΖ®±μ ΨΜΕΜΕΥφΜζΒΊ¥”Ήά…œ»Γ≥ωΝΫΗωάώΑϋΒΡΥυ”–Ω…ΡήΫαΙϊΘ§≤Δ«σ»Γ≥ωΒΡΝΫΗωάώΑϋΕΦ «÷«ΡήΕ‘ΜΑΜζΤς»ΥΒΡΗ≈¬ .
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί“ΜΙ≤»ΐΗωάώΑϋΘ§Α≈±»ΆόΆόΒΡάώΑϋ’Φ“Μ÷÷Φ¥Ω…ΦΤΥψΗ≈¬ ΘΜ
Θ®2Θ©Ν–≥ωΥυ”–Ω…ΡήΒΡΫαΙϊΘ§‘Ό’“ΒΫΖϊΚœ“Σ«σΒΡΗω ΐΘ§Φ¥Ω…ΒΟΒΫΗ≈¬ .
Θ®1Θ©ΗυΨίΧβ“βΘ§Ω…÷Σ»Γ≥ωΒΡ «Α≈±»ΆόΆόΒΡΗ≈¬ «![]() .
.
Θ®2Θ©
ΫαΙϊΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
”…ΆΦΩ…÷ΣΘ§Ι≤”–6÷÷Β»Ω…ΡήΒΡΫαΙϊΘ§ΕχΖϊΚœ“Σ«σΒΡ «![]() Θ§
Θ§![]() ΝΫ÷÷Θ§
ΝΫ÷÷Θ§
Γύ»Γ≥ωΒΡΝΫΗωάώΑϋΕΦ «÷«ΡήΜζΤς»ΥΒΡΗ≈¬ «![]() .
.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
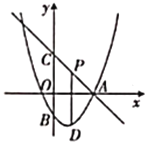
ΓΨΧβΡΩΓΩΕΞΒψΈΣDΒΡ≈ΉΈοœΏyΘΫ©¹x2+bx+cΫΜx÷α”ΎAΓΔB(3Θ§0)Θ§ΫΜy÷α”ΎΒψCΘ§÷±œΏyΘΫ©¹![]() x+mΨ≠ΙΐΒψCΘ§ΫΜx÷α”ΎE(4Θ§0)Θ°
x+mΨ≠ΙΐΒψCΘ§ΫΜx÷α”ΎE(4Θ§0)Θ°
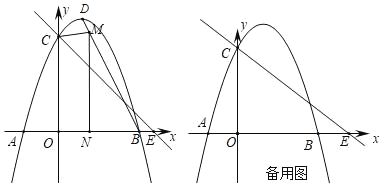
(1)«σ≥ω≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
(2)»γΆΦ1Θ§ΒψMΈΣœΏΕΈBD…œ≤Μ”κBΓΔD÷ΊΚœΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψMΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣNΘ§…ηΒψMΒΡΚαΉχ±ξΈΣxΘ§ΥΡ±Ώ–ΈOCMNΒΡΟφΜΐΈΣSΘ§«σS”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σSΒΡΉν¥σ÷ΒΘΜ
(3)ΒψPΈΣx÷αΒΡ’ΐΑκ÷α…œ“ΜΗωΕ·ΒψΘ§ΙΐPΉςx÷αΒΡ¥ΙœΏΘ§ΫΜ÷±œΏyΘΫ©¹![]() x+m”ΎGΘ§ΫΜ≈ΉΈοœΏ”ΎHΘ§Ν§Ϋ”CHΘ§ΫΪΓςCGH―ΊCHΖ≠’έΘ§»τΒψGΒΡΕ‘”ΠΒψF«ΓΚΟ¬δ‘Ύy÷α…œ ±Θ§«κ÷±Ϋ”–¥≥ωΒψPΒΡΉχ±ξΘ°
x+m”ΎGΘ§ΫΜ≈ΉΈοœΏ”ΎHΘ§Ν§Ϋ”CHΘ§ΫΪΓςCGH―ΊCHΖ≠’έΘ§»τΒψGΒΡΕ‘”ΠΒψF«ΓΚΟ¬δ‘Ύy÷α…œ ±Θ§«κ÷±Ϋ”–¥≥ωΒψPΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥…Χ≥ΓΨ≠ –≥ΓΒς≤ιΘ§ΖΔœ÷ΫχΦέΈΣ40‘ΣΒΡΧ®ΒΤΟΩ‘¬ΒΡœζ έΝΩyΘ®Χ®Θ©”κ έΦέxΘ®‘ΣΘ©ΒΡœύΙΊ–≈œΔ»γœ¬ΘΚ
έΦέxΘ®‘ΣΘ© | 50 | 60 | 70 | 80 | Γ≠Γ≠ |
œζ έΝΩyΘ®Χ®Θ© | 200 | 180 | 160 | 140 | Γ≠Γ≠ |
Θ®1Θ© ‘”ΟΡψ―ßΙΐΒΡΚ· ΐά¥Οη ωy”κxΒΡΙΊœΒΘ§’βΗωΚ· ΐΩ…“‘ «ΓΓ Κ· ΐΘ§«σ’βΗωΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ© έΦέΈΣΕύ…Ό‘Σ ±Θ§Β±‘¬ΒΡάϊ»σΉν¥σΘΩΉν¥σάϊ»σ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
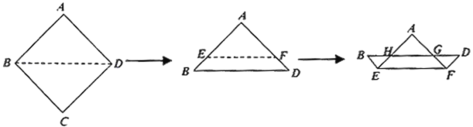
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΫΪ“Μ’≈’ΐΖΫ–Έ÷ΫΤ§![]() Θ§“ά¥Έ―ΊΉ≈’έΚέ
Θ§“ά¥Έ―ΊΉ≈’έΚέ![]() Θ§
Θ§![]() Θ®Τδ÷–
Θ®Τδ÷–![]() Θ©œρ…œΖ≠’έΝΫ¥ΈΘ§–Έ≥…ΓΑ–Γ¥§Γ±ΒΡΆΦ―υΘ°»τ
Θ©œρ…œΖ≠’έΝΫ¥ΈΘ§–Έ≥…ΓΑ–Γ¥§Γ±ΒΡΆΦ―υΘ°»τ![]() Θ§ΥΡ±Ώ–Έ
Θ§ΥΡ±Ώ–Έ![]() ”κ
”κ![]() ΒΡ÷ή≥Λ≤νΈΣ
ΒΡ÷ή≥Λ≤νΈΣ![]() Θ§‘ρ’ΐΖΫ–Έ
Θ§‘ρ’ΐΖΫ–Έ![]() ΒΡ÷ή≥ΛΈΣ______Θ°
ΒΡ÷ή≥ΛΈΣ______Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
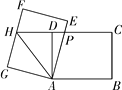
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–ΈABCD÷–Θ§ABΘΫ8Θ§BCΘΫ6Θ§ΫΪΨΊ–ΈABCD»ΤΒψAΡφ ±’κ–ΐΉΣΒΟΒΫΨΊ–ΈAEFGΘ§AEΘ§FGΖ÷±πΫΜ…δœΏCD”ΎΒψPΘ§HΘ§Ν§Ϋ”AHΘ§»τΒψP «CHΒΡ÷–ΒψΘ§‘ρΓςAPHΒΡ÷ή≥ΛΈΣ_____
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏ![]() ΫΜ
ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§≈ΉΈοœΏ
Θ§≈ΉΈοœΏ![]() Ψ≠ΙΐΒψ
Ψ≠ΙΐΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() ΈΣ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ§ΙΐΒψ
ΈΣ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ§ΙΐΒψ![]() Ής
Ής![]() ÷αΒΡ¥ΙœΏΘ§ΫΜ÷±œΏ
÷αΒΡ¥ΙœΏΘ§ΫΜ÷±œΏ![]() ”ΎΒψ
”ΎΒψ![]() Θ§…ηΒψ
Θ§…ηΒψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]() .
.
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω Ϋ.
Θ®2Θ©Β±Βψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() œ¬ΖΫΒΡ≈ΉΈοœΏ…œ‘ΥΕ· ±Θ§«σ≥ω
œ¬ΖΫΒΡ≈ΉΈοœΏ…œ‘ΥΕ· ±Θ§«σ≥ω![]() ≥ΛΕ»ΒΡΉν¥σ÷Β.
≥ΛΕ»ΒΡΉν¥σ÷Β.
Θ®3Θ©Β±“‘![]() Θ§
Θ§![]() Θ§
Θ§![]() ΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–Έ ±Θ§«σ¥Υ ±
ΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–Έ ±Θ§«σ¥Υ ±![]() ΒΡ÷Β.
ΒΡ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§÷±œΏ![]() ”κΥΪ«ζœΏ
”κΥΪ«ζœΏ![]() Θ®x>0Θ©ΫΜ”ΎΒψ
Θ®x>0Θ©ΫΜ”ΎΒψ![]() Θ°
Θ°
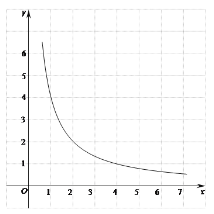
Θ®1Θ©«σaΘ§kΒΡ÷ΒΘΜ
Θ®2Θ©“―÷Σ÷±œΏ![]() ΙΐΒψ
ΙΐΒψ![]() «“ΤΫ––”Ύ÷±œΏ
«“ΤΫ––”Ύ÷±œΏ![]() Θ§ΒψPΘ®mΘ§nΘ©Θ®m>3Θ© «÷±œΏ
Θ§ΒψPΘ®mΘ§nΘ©Θ®m>3Θ© «÷±œΏ![]() …œ“ΜΕ·ΒψΘ§ΙΐΒψPΖ÷±πΉς
…œ“ΜΕ·ΒψΘ§ΙΐΒψPΖ÷±πΉς![]() ÷αΓΔ
÷αΓΔ![]() ÷αΒΡΤΫ––œΏΘ§ΫΜΥΪ«ζœΏ
÷αΒΡΤΫ––œΏΘ§ΫΜΥΪ«ζœΏ![]() Θ®x>0Θ©”ΎΒψ
Θ®x>0Θ©”ΎΒψ![]() ΓΔ
ΓΔ![]() Θ§ΥΪ«ζœΏ‘ΎΒψMΓΔN÷°ΦδΒΡ≤ΩΖ÷”κœΏΕΈPMΓΔPNΥυΈß≥…ΒΡ«χ”ρΘ®≤ΜΚ§±ΏΫγΘ©Φ«ΈΣ
Θ§ΥΪ«ζœΏ‘ΎΒψMΓΔN÷°ΦδΒΡ≤ΩΖ÷”κœΏΕΈPMΓΔPNΥυΈß≥…ΒΡ«χ”ρΘ®≤ΜΚ§±ΏΫγΘ©Φ«ΈΣ![]() Θ°ΚαΓΔΉίΉχ±ξΕΦ «’ϊ ΐΒΡΒψΫ–Ήω’ϊΒψΘ°
Θ°ΚαΓΔΉίΉχ±ξΕΦ «’ϊ ΐΒΡΒψΫ–Ήω’ϊΒψΘ°
ΔΌΒ±![]() ±Θ§÷±Ϋ”–¥≥ω«χ”ρ
±Θ§÷±Ϋ”–¥≥ω«χ”ρ![]() ΡΎΒΡ’ϊΒψΗω ΐΘΜΔΎ»τ«χ”ρ
ΡΎΒΡ’ϊΒψΗω ΐΘΜΔΎ»τ«χ”ρ![]() ΡΎΒΡ’ϊΒψΗω ΐ≤Μ≥§Ιΐ8ΗωΘ§ΫαΚœΆΦœσΘ§«σmΒΡ»Γ÷ΒΖΕΈßΘ°
ΡΎΒΡ’ϊΒψΗω ΐ≤Μ≥§Ιΐ8ΗωΘ§ΫαΚœΆΦœσΘ§«σmΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΨΊ–ΈABCDΒΡ÷ή≥ΛΈΣ12Θ§EΘ§FΘ§GΘ§HΈΣΨΊ–ΈABCDΒΡΗς±Ώ÷–ΒψΘ§»τABΘΫxΘ§ΥΡ±Ώ–ΈEFGHΒΡΟφΜΐΈΣy.
(1)«κ÷±Ϋ”–¥≥ωy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
(2)ΗυΨί(1)÷–ΒΡΚ· ΐΙΊœΒ ΫΘ§ΦΤΥψΒ±xΈΣΚΈ÷Β ±Θ§yΉν¥σΘ§≤Δ«σ≥ωΉν¥σ÷ΒΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§‘ΎΥΡ±Ώ–ΈABCD÷–Θ§ABΓΈCDΘ§Ε‘Ϋ«œΏACΓΔBDΫΜ”ΎΒψEΘ§ΒψF‘Ύ±ΏAB…œΘ§Ν§Ϋ”CFΫΜœΏΕΈBE”ΎΒψGΘ§CG2=GEGDΘ°
Θ®1Θ©«σ÷ΛΘΚΓœACF=ΓœABDΘΜ
Θ®2Θ©Ν§Ϋ”EFΘ§«σ÷ΛΘΚEFCG=EGCBΘ°
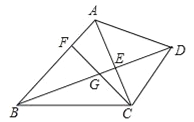
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com