
【题目】某商场经市场调查,发现进价为40元的台灯每月的销售量y(台)与售价x(元)的相关信息如下:
售价x(元) | 50 | 60 | 70 | 80 | …… |
销售量y(台) | 200 | 180 | 160 | 140 | …… |
(1)试用你学过的函数来描述y与x的关系,这个函数可以是 函数,求这个函数关系式;
(2)售价为多少元时,当月的利润最大?最大利润是多少?
【答案】(1)一次函数; (2)当售价定为95元时,利润最大,最大值为6050元.
【解析】
(1)由x的值每增加10元时,y的值均减小20件知这个函数为一次函数,待定系数法求解可得;
(2)根据“总利润=单件利润×销售量”列出函数解析式,再配方成顶点式,依据二次函数的性质是解题的关键.
解:(1)由表可知,x的值每增加10元时,y的值均减小20件,
据此可知y与x的函数关系为一次函数;
设该一次函数为y=k x+b,代入(50,200)和(60,180),
得:![]() ,解得
,解得![]() ,
,
∴y=-2x+300,
将(70,160),(80,140)代入上式等式成立;
(2)设月利润为w元,则w=(x-40) y,即w=(x-40) (-2x+300),
配方得:w=﹣2(x﹣95)2+6050,
∵﹣2<0,∴当x=95时,w有最大值6050
答:当售价定为95元时,利润最大,最大值为6050元.


科目:初中数学 来源: 题型:
【题目】如图在菱形纸片ABCD中,AB=4,∠B=120°,将菱形纸片翻折,使点A落在边CD的中点G处,折痕为EF,点E,F分别在边AD,AB上,则sin∠GEF的值为_____.
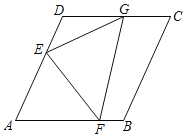
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实视力保护工作,某校组织七年级学生开展了视力保健活动.活动前随机测查了30名学生的视力,活动后再次测查这部分学生的视力.两次相关数据记录如下:
活动前被测查学生视力数据:
![]()
活动后被测查学生视力数据:
![]()
活动后被测查学生视力频数分布表
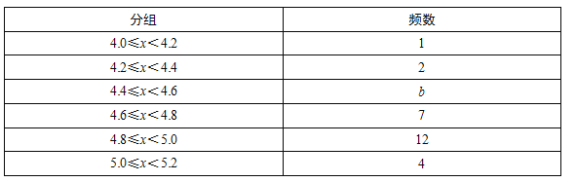
根据以上信息回答下列问题:
(1)填空:a= ,b= ,活动前被测查学生视力样本数据的中位数是 ,活动后被测查学生视力样本数据的众数是 ;
(2)若视力在4.8及以上为达标,估计七年级600名学生活动后视力达标的人数有多少?
(3)分析活动前后相关数据,从一个方面评价学校开展视力保健活动的效果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是一张等腰直角三角形板,
是一张等腰直角三角形板,![]() ,要在这张纸板中剪取正方形(剪法如图1所示),图1中剪法称为第
,要在这张纸板中剪取正方形(剪法如图1所示),图1中剪法称为第![]() 次剪取,记所得的正方形面积为
次剪取,记所得的正方形面积为![]() ;按照图1中的剪法,在余下的
;按照图1中的剪法,在余下的![]() 和
和![]() 中,分别剪取两个全等正方形,称为第
中,分别剪取两个全等正方形,称为第![]() 次剪取,并记这两个正方形面积和为
次剪取,并记这两个正方形面积和为![]() ,(如图2) ;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第
,(如图2) ;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第![]() 次剪取,并记这四个正方形的面积和为
次剪取,并记这四个正方形的面积和为![]() ,(如图3);继续操作下去···则第
,(如图3);继续操作下去···则第![]() 次剪取后,
次剪取后,![]() ___________.
___________.
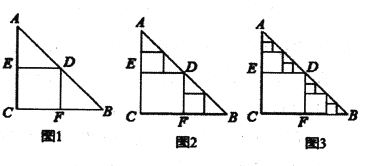
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆![]() 是锐角
是锐角![]() 的外接圆,
的外接圆,![]() 是弧
是弧![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,则有下列结论:①点
,则有下列结论:①点![]() 是
是![]() 的重心;②
的重心;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的序号是__________.
,其中正确结论的序号是__________.
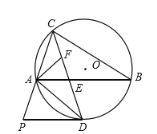
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”译文:已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?(1丈=10尺,1尺=10寸)设长方形门的宽![]() 尺,可列方程为_______.
尺,可列方程为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,将点
,将点![]() 向左平移6个单位长度,得到点
向左平移6个单位长度,得到点![]() .
.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若抛物线![]() 经过点
经过点![]() ,
,![]() ,求抛物线的表达式;
,求抛物线的表达式;
(3)若抛物线![]() 的顶点在直线
的顶点在直线![]() 上移动,当抛物线与线段
上移动,当抛物线与线段![]() 有2个公共点时,求抛物线顶点横坐标
有2个公共点时,求抛物线顶点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】欢欢放学回家看到桌上有三个礼包,是爸爸送给欢欢和姐姐的礼物,其中![]() 礼包是芭比娃娃,
礼包是芭比娃娃,![]() 和
和![]() 礼包都是智能对话机器人.这些礼包用外表一样的包装盒装着,看不到里面的礼物.
礼包都是智能对话机器人.这些礼包用外表一样的包装盒装着,看不到里面的礼物.
(1)欢欢随机地从桌上取出一个礼包,取出的是芭比娃娃的概率是多少?
(2)请用树状图或列表法表示欢欢随机地从桌上取出两个礼包的所有可能结果,并求取出的两个礼包都是智能对话机器人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为全面贯彻党的教育方针,坚持“健康第一的教育理念,促进学生健康成长,提高体质健康水平,成都市调整体育中考实施方案:分值增加至60,男1000(女80米)必考,足球、篮球、排球“三选一”……从2019年秋季新入学的七年级起开始实施,某1学为了解七年级学生对三大球类运动的喜爱情况,从七年级学生中随机抽取部分学生进行调查问卷,通过分析整理绘制了如下两幅统计图。请根据两幅统计图中的信息回答下列问题:
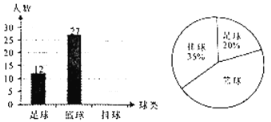
(1)求参与调查的学生中,喜爱排球运动的学生人数,并补全条形图
(2)若该中学七年级共有400名学生,请你估计该中学七年级学生中喜爱篮球运动的学生有多少名?
(3)若从喜爱足球运动的2名男生和2名女生中随机抽取2名学生,确定为该校足球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com