
����Ŀ����֪![]() ��һ�ŵ���ֱ�������ΰ壬
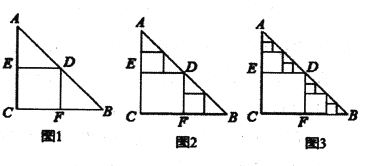
��һ�ŵ���ֱ�������ΰ壬![]() ��Ҫ������ֽ���м�ȡ������(������ͼ1��ʾ)��ͼ1�м�����Ϊ��
��Ҫ������ֽ���м�ȡ������(������ͼ1��ʾ)��ͼ1�м�����Ϊ��![]() �μ�ȡ�������õ����������Ϊ
�μ�ȡ�������õ����������Ϊ![]() ������ͼ1�еļ����������µ�
������ͼ1�еļ����������µ�![]() ��
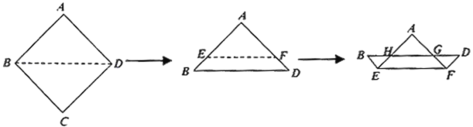
��![]() �У��ֱ��ȡ����ȫ�������Σ���Ϊ��
�У��ֱ��ȡ����ȫ�������Σ���Ϊ��![]() �μ�ȡ�����������������������Ϊ
�μ�ȡ�����������������������Ϊ![]() ��(��ͼ2) ���������µ��ĸ��������У���ͬ���ķ����ֱ��ȡ�����Σ��õ��ĸ���ͬ�������Σ���Ϊ��
��(��ͼ2) ���������µ��ĸ��������У���ͬ���ķ����ֱ��ȡ�����Σ��õ��ĸ���ͬ�������Σ���Ϊ��![]() �μ�ȡ���������ĸ������ε������Ϊ
�μ�ȡ���������ĸ������ε������Ϊ![]() ��(��ͼ3)������������ȥ���������
��(��ͼ3)������������ȥ���������![]() �μ�ȡ��
�μ�ȡ��![]() ___________��
___________��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90������б��AB��һ��OΪԲ�ģ�OBΪ�뾶����O����AC�ڵ�E����AB�ڵ�D���ҡ�BEC=��BDE��

��1����֤��AC�ǡ�O�����ߣ�
��2������OC��BE�ڵ�F����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ΪD��������y����x2+bx+c��x����A��B(3��0)����y���ڵ�C��ֱ��y����![]() x+m������C����x����E(4��0)��
x+m������C����x����E(4��0)��
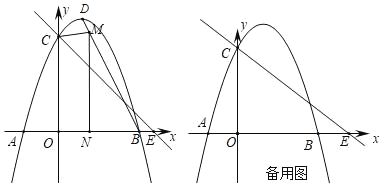
(1)��������ߵĽ���ʽ��
(2)��ͼ1����MΪ�߶�BD�ϲ���B��D�غϵ�һ�����㣬����M��x��Ĵ��ߣ�����ΪN�����M�ĺ�����Ϊx���ı���OCMN�����ΪS����S��x֮��ĺ�����ϵʽ������S�����ֵ��
(3)��PΪx�����������һ�����㣬��P��x��Ĵ��ߣ���ֱ��y����![]() x+m��G������������H������CH������CGH��CH���ۣ�����G�Ķ�Ӧ��Fǡ������y����ʱ����ֱ��д����P�����꣮
x+m��G������������H������CH������CGH��CH���ۣ�����G�Ķ�Ӧ��Fǡ������y����ʱ����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
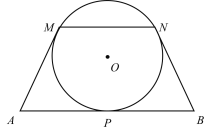
����Ŀ����ͼ��AB��AM��BN �ֱ��ǡ�O �����ߣ��е�ֱ�Ϊ P��M��N���� MN��AB����A��60����AB��6�����O �İ뾶�ǣ� ��
A.![]() B.3C.
B.3C.![]()
![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��m Ϊ��������
��m ��������
��1��֤�������� m Ϊ��ֵ���ú�����ͼ���� x ���������������㣻
��2���� m ��ֵ�ı�ʱ���ú�����ͼ���� x ������������֮��ľ����Ƿ�ı䣿�����䣬 ��������룻���ı䣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�������ⷢ�֣�
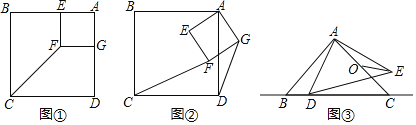
��ͼ����������AEFG�����߷ֱ���������ABCD�ı�AB��AD�ϣ�����CF��
��գ����߶�CF��DG��������ϵΪ�� ����
��ֱ��CF��DG������ǵĶ���Ϊ�� ����
��2������չ̽����
��ͼ������������AEFG�Ƶ�A��ʱ����ת������ת�Ĺ����У���1���еĽ����Ƿ���Ȼ������������ͼ������˵����
��3��������⣩
��ͼ������ABC�͡�ADE���ǵ���ֱ�������Σ���BAC����DAE��90�㣬AB��AC��4��OΪAC���е㣮����D��ֱ��BC���˶�������OE�����ڵ�D���˶������У��߶�OE������СֵΪ�� ����ֱ��д���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳����г����飬���ֽ���Ϊ40Ԫ��̨��ÿ�µ�������y��̨�����ۼ�x��Ԫ���������Ϣ���£�
�ۼ�x��Ԫ�� | 50 | 60 | 70 | 80 | ���� |
������y��̨�� | 200 | 180 | 160 | 140 | ���� |
��1��������ѧ���ĺ���������y��x�Ĺ�ϵ����������������� �����������������ϵʽ��
��2���ۼ�Ϊ����Ԫʱ�����µ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��������ֽƬ![]() �����������ۺ�
�����������ۺ�![]() ��
��![]() ������
������![]() �����Ϸ������Σ��γɡ�С������ͼ������
�����Ϸ������Σ��γɡ�С������ͼ������![]() ���ı���
���ı���![]() ��
��![]() ���ܳ���Ϊ
���ܳ���Ϊ![]() ����������
����������![]() ���ܳ�Ϊ______��
���ܳ�Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD���ܳ�Ϊ12��E��F��G��HΪ����ABCD�ĸ����е�����AB��x���ı���EFGH�����Ϊy.
(1)��ֱ��д��y��x֮��ĺ�����ϵʽ��
(2)����(1)�еĺ�����ϵʽ�����㵱xΪ��ֵʱ��y�������������ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com