
【题目】如图,在矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点P,H,连接AH,若点P是CH的中点,则△APH的周长为_____
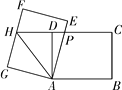
【答案】20
【解析】
设HD=x,然后表示出HC,HP,根据等面积法得出HP=AP,然后在Rt△APD中利用勾股定理求出x的值,进而可求出HP的长度,然后在Rt△ADH中求出HA的长度,则△APH的周长可求.
设HD=x,由题意得HC=x+8.
∵点P是CH的中点,
∴HP=![]() =4+
=4+![]() x.
x.
由题图可知,在△HPA中,边HP和边AP上的高相等,
∴由面积法得HP=AP.
∴AP=4+![]() x.
x.
∵DP=HP-HD=4-![]() x,
x,
∴在Rt△APD中,AP2=DP2+AD2.
∴(4+![]() x)2=(4-
x)2=(4-![]() x)2+62.
x)2+62.
解得x=![]() .
.
∴HP=4+![]() ×
×![]() =
=![]() .
.
∴在Rt△ADH中,HA=![]() =
=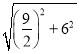 =
=![]() .
.
∴△APH的周长为![]() +
+![]() ×2=20.
×2=20.
故答案为:20.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
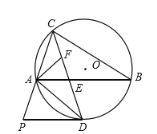
【题目】如图,圆![]() 是锐角
是锐角![]() 的外接圆,
的外接圆,![]() 是弧
是弧![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,则有下列结论:①点
,则有下列结论:①点![]() 是
是![]() 的重心;②
的重心;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论的序号是__________.
,其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,将点
,将点![]() 向左平移6个单位长度,得到点
向左平移6个单位长度,得到点![]() .
.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若抛物线![]() 经过点
经过点![]() ,
,![]() ,求抛物线的表达式;
,求抛物线的表达式;
(3)若抛物线![]() 的顶点在直线
的顶点在直线![]() 上移动,当抛物线与线段
上移动,当抛物线与线段![]() 有2个公共点时,求抛物线顶点横坐标
有2个公共点时,求抛物线顶点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,在![]() 中,把
中,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() (
(![]() )并延长一倍得到
)并延长一倍得到![]() ,把
,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 并延长一倍得到
并延长一倍得到![]() ,连接
,连接![]() .当
.当![]() 时,称
时,称![]() 是
是![]() 的“倍旋三角形”,
的“倍旋三角形”,![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“倍旋中线”.
的“倍旋中线”.
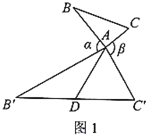
特例感知:
(1)如图1,当![]() ,
,![]() 时,则“倍旋中线”
时,则“倍旋中线”![]() 长为______;如图2,当
长为______;如图2,当![]() 为等边三角形时,“倍旋中线”
为等边三角形时,“倍旋中线”![]() 与
与![]() 的数量关系为______;
的数量关系为______;
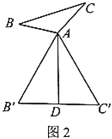
猜想论证:
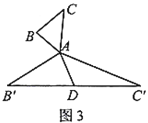
(2)在图3中,当![]() 为任意三角形时,猜想“倍旋中线”
为任意三角形时,猜想“倍旋中线”![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】欢欢放学回家看到桌上有三个礼包,是爸爸送给欢欢和姐姐的礼物,其中![]() 礼包是芭比娃娃,
礼包是芭比娃娃,![]() 和
和![]() 礼包都是智能对话机器人.这些礼包用外表一样的包装盒装着,看不到里面的礼物.
礼包都是智能对话机器人.这些礼包用外表一样的包装盒装着,看不到里面的礼物.
(1)欢欢随机地从桌上取出一个礼包,取出的是芭比娃娃的概率是多少?
(2)请用树状图或列表法表示欢欢随机地从桌上取出两个礼包的所有可能结果,并求取出的两个礼包都是智能对话机器人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】改革开放以来,由于各阶段发展重心不同,某市的需求结构经历了消费投资交替主导、投资消费双轮驱动到消费主导的变化.到2007年,某市消费率超过投资率,标志着某市经济增长由投资消费双轮驱动向消费趋于主导过渡.下图是某市1978—2017年投资率与消费率统计图.根据统计图回答:________年,某市消费率与投资率相同;从2000年以后,某市消费率逐年上升的时间段是________.
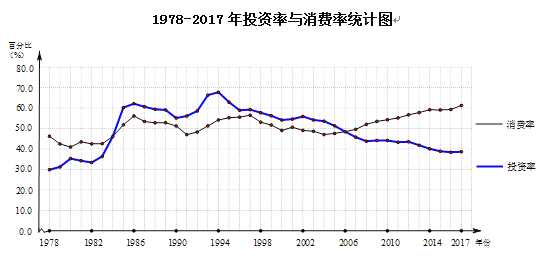
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块长为22 m,宽为17 m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300 m2.若设道路宽为x m,根据题意可列出方程为______________________________.
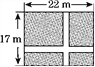
【答案】(22-x)(17-x)=300(或x2-39x+74=0)
【解析】试题分析:把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的草坪是一个长方形,根据长方形的面积公式列方程.设道路的宽应为x米,由题意有(22﹣x)(17﹣x)=300,故答案为:(22﹣x)(17﹣x)=300.
考点:由实际问题抽象出一元二次方程.
【题型】填空题
【结束】
17
【题目】x=1是关于x的一元二次方程x2+mx﹣5=0的一个根,则此方程的另一个根是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com