
【题目】为了迎接“5.1”小长假的购物高峰,大冶雨润某运动品牌服装店准备购进甲、乙两种服装,已知每件甲服装进价比每件乙服装进价多20元,售价在进价的基础上加价50%,通过初步预算,若以4800元购进的甲服装比以4200元购进乙服装的件数少10件.
(1)求甲、乙两种服装的销售单价.
(2)现老板计划购进两种服装共100件,其中甲种服装不少于65件,若购进这100件服装的费用不超过7500元,则甲种服装最多购进多少件?
【答案】(1)每件甲服装的销售单价为120元,每件乙服装的销售单价为90元;(2)甲种服装最多购进75件.
【解析】
(1)设每件乙服装的进价为x元,则每件甲服装的进价为(x+20)元,根据数量=总价÷单价结合以4800元购进的甲服装比以4200元购进乙服装的件数少10件,即可得出关于x的分式方程,解之经检验后即可得出x的值,再结合售价在进价的基础上加价50%即可求出结论;
(2)设购进m件甲种服装,则购进(100-m)件乙种服装,根据购进的甲种服装不少于65件且购进这100件服装的费用不超过7500元,即可得出关于m的一元一次不等式组,解之取其中的最大值即可得出结论.
(1)设每件乙服装的进价为x元,则每件甲服装的进价为(x+20)元,
依题意,得: ![]()
化简,得:x2+80x﹣8400=0,
解得:x1=﹣140,x2=60,
经检验,x1=﹣140,x2=60是原方程的解,x1=﹣140不符合题意,舍去,x2=60符合题意,
∴x+20=80,
∴(1+50%)×60=90(元),(1+50%)×80=120(元).
答:每件甲服装的销售单价为120元,每件乙服装的销售单价为90元.
(2)设购进m件甲种服装,则购进(100﹣m)件乙种服装,
依题意,得:
解得:65≤m≤75.
答:甲种服装最多购进75件.


科目:初中数学 来源: 题型:
【题目】如图,在同一平面内,两条平行的高速公路AB和CD之间有一条“L”型道路连通,“L”型道路中的EP=FP=20千米,∠BEP=12°,∠EPF=80°,求AB和CD之间的距离.(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
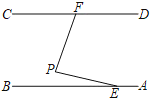
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示抛物线![]() 过点
过点![]() ,点
,点![]() ,且
,且![]()
(1)求抛物线的解析式及其对称轴;
(2)点![]() 在直线
在直线![]() 上的两个动点,且
上的两个动点,且![]() ,点
,点![]() 在点
在点![]() 的上方,求四边形
的上方,求四边形![]() 的周长的最小值;
的周长的最小值;
(3)点![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,直线
,直线![]() 把四边形
把四边形![]() 的面积分为3∶5两部分,求点
的面积分为3∶5两部分,求点![]() 的坐标.
的坐标.
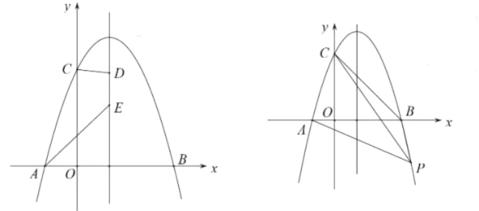
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=4![]() ,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
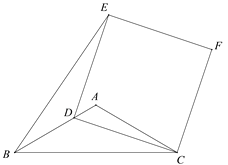
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a≠0)的图象如图所示,则下列结论中正确的是
(a≠0)的图象如图所示,则下列结论中正确的是
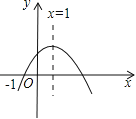
A. a>0 B. 当﹣1<x<3时,y>0
C. c<0 D. 当x≥1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“世界读书日”前夕,某校开展了“读书助我成长”的阅读活动.为了了解该校学生在此次活动中课外阅读书籍的数量情况,随机抽取了部分学生进行调查,将收集到的数据进行整理,绘制出两幅不完整的统计图,请根据统计图信息解决下列问题:
(1)求本次调查中共抽取的学生人数;
(2)补全条形统计图;
(3)在扇形统计图中,阅读![]() 本书籍的人数所在扇形的圆心角度数是 ;
本书籍的人数所在扇形的圆心角度数是 ;
(4)若该校有![]() 名学生,估计该校在这次活动中阅读书籍的数量不低于
名学生,估计该校在这次活动中阅读书籍的数量不低于![]() 本的学生有多少人?
本的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
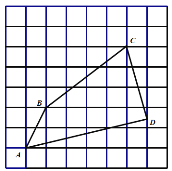
【题目】如图,在每个小正方形的边长为的网格中,点![]() 均在格点上,
均在格点上,![]() 为小正方形边中点.
为小正方形边中点.
(1)![]() 的长等于 ______;
的长等于 ______;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个点![]() ,使其满足
,使其满足![]() 说明点
说明点![]() 的位置是如何找到的(不要求证明)______.
的位置是如何找到的(不要求证明)______.
查看答案和解析>>
科目:初中数学 来源: 题型:
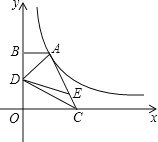
【题目】如图,点A在双曲线y=![]() (k≠0)的第一象限的分支上,AB垂直y轴于点B,点C在x轴正半轴上,OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,连接CD,若△CDE的面积为1,则k的值为_____.
(k≠0)的第一象限的分支上,AB垂直y轴于点B,点C在x轴正半轴上,OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,连接CD,若△CDE的面积为1,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受疫情的影响,很多农产品滞销,各大电商发起了“爱心助农”活动,帮助农户进行农产品销售.已知某种橘子的成本为4元/千克,经过市场调查发现,一天内橘子的销售量y(千克)与销售单价x(元/千克)(4≤x≤10)的函数关系如下图所示:

(1)当4≤x≤8时,求y与x的函数解析式;
(2)当4≤x≤8时,要使一天内获得的利润为1200元,单价应定为多少?
(3)求橘子的单价定为多少时,一天内获得的利润最大,最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com