
【题目】如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题:
①四边形ABCD是菱形;
②四边形ABCD是中心对称图形;
③四边形ABCD是轴对称图形;
④AC=BD.
其中正确的是(写上正确的序号).
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】把下列各数的序号填到相应的横线上:
①+5,②-3,③0,④-1.414,⑤17,⑥-![]() .
.
正整数:______________________________________________________;
负分数:______________________________________________________;
负有理数:____________________________________________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求解下列方程.
(1)(x﹣3)2=16
(2)x2﹣4x=5(配方法)
(3)x2﹣4x﹣5=0(公式法)
(4)x2﹣5x=0(因式分解法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
①a<0,b<0,
②2a﹣b>0,
③a+b+c>0,
④a﹣b+c<0,
⑤当x>1时,y随x的增大而减小,
其中正确的是( )
A.①②③
B.②③④
C.③④⑤
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)x2﹣2x﹣8=0;
(2)3x(x﹣1)=2(x﹣1);
(3)x2+3=3(x+1);
(4)2x(4x+5)=7;
(5)4x2﹣8x+1=0;
(6)(y+2)2=(3y﹣1)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正△ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB. 
(1)求旋转角的度数;
(2)求点P与点P′之间的距离;
(3)求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
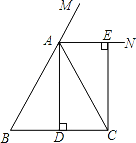
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2﹣4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当0≤x≤3时,y2的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com