Question

【题目】Rt△ABC中，∠BAC=90°，AB=AC=2．以AC为一边，在△ABC外部作等腰直角三角形ACD，则线段BD的长为_____．

Answer 1

【答案】4或2或．

【解析】

试题分情况讨论，①以A为直角顶点，向外作等腰直角三角形DAC；②以C为直角顶点，向外作等腰直角三角形ACD；③以AC为斜边，向外作等腰直角三角形ADC．分别画图，并求出BD．

解：①以A为直角顶点，向外作等腰直角三角形DAC，

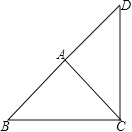
∵∠DAC=90°，且AD=AC，

∴BD=BA+AD=2+2=4；

②以C为直角顶点，向外作等腰直角三角形ACD，

连接BD，过点D作DE⊥BC，交BC的延长线于E．

∵△ABC是等腰直角三角形，∠ACD=90°，

∴∠DCE=45°，

又∵DE⊥CE，

∴∠DEC=90°，

∴∠CDE=45°，

∴CE=DE=2×=，

在Rt△BAC中，BC==2，

∴BD===2；

③以AC为斜边，向外作等腰直角三角形ADC，

∵∠ADC=90°，AD=DC，且AC=2，

∴AD=DC=ACsin45°=2×=，

又∵△ABC、△ADC是等腰直角三角形，

∴∠ACB=∠ACD=45°，

∴∠BCD=90°，

又∵在Rt△ABC中，BC==2，

∴BD===．

故BD的长等于4或2或．