
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示. 
(1)求这个二次函数的解析式;
(2)根据图象,写出当x取何值时,y>0?
【答案】
(1)解:∵图象过(﹣3,0),(1,0),
∴设抛物线的解析式为y=a(x+3)(x﹣1)(a≠0),
∵图象过(0,3),
∴3=a(0+3)(0﹣1),
a=﹣1,
∴y=﹣(x+3)(x﹣1),
即y=﹣x2﹣2x+3
(2)解:由图象可知,当﹣3<x<1,y>0
【解析】(1)设抛物线的解析式为y=a(x+3)(x﹣1)(a≠0),图象过点(0,3),求出a的值,即可求出二次函数的解析式;(2)直接根据图象写出x的取值范围.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
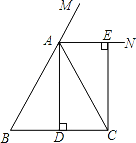
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O上有两点A与P,且OA⊥OP,若A点固定不动,P点在圆上匀速运动一周,那么弦AP的长度d与时间t的函数关系的图象可能是( )

A.①
B.③
C.①或③
D.②或④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作图的切线。
已知:P为圆O外一点。
求作:经过点P的圆O的切线。
小敏的作法如下:
①连接OP,作线段OP的垂直平分线MN交OP于点C;
②以点C为圆心,CO的长为半径作圆交圆O于A、B两点;
③作直线PA、PB,所以直线PA、PB就是所求作的切线。
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在数轴上点A表示数a,点B表示数b,且a,b满足![]() .
.
(1)点A表示的数为________,点B表示的数为________;
(2)设点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.若在数轴上存在一点C,使BC=2AC,则点C表示的数为__________;
(3)若在原点处放一挡板,一小球甲从点A处以每秒2个单位长度的速度向左运动;同时另一小球乙从点B以每秒2个单位长度的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)以原来速度的两倍向相反的方向运动.设运动的时间为t秒,请用含t的代数式分别表示出甲、乙两小球到原点的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2﹣4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2与y1为“同簇二次函数”,求函数y2的表达式,并求出当0≤x≤3时,y2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点F为弦AC的中点,连接OF并延长交⊙O于点D,过点D作⊙O的切线,交BA的延长线于点E. 
(1)求证:AC∥DE;
(2)若OA=AE=4,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D. 
(1)求证:CD=CB;
(2)如果⊙O的半径为 ![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com