
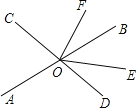
【题目】直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,垂足为O.
(1)若∠EOF=54°,求∠AOC的度数;
(2)①在∠AOD的内部作射线OG⊥OE;
②试探索∠AOG与∠EOF之间有怎样的关系?并说明理由.
【答案】(1)∠AOC=72°;(2)∠AOG=∠EOF
【解析】试题分析:(1)利用角平分线的性质结合已知得出∠DOE的度数,进而得出答案;
(2)①根据要求作图即可;
②由OG⊥OE得∠AOG+∠GOE+∠BOE=180°,由OF⊥CD得∠COF+∠FOE+∠DOE= 180°,又OE是角平分线,即可得出结论.
试题解析:(1)∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵∠EOF=54°,OD⊥OF,
∴∠DOE=36°,
∴∠BOE=36°,
∴∠AOC=72°;
(2)①如图所示,
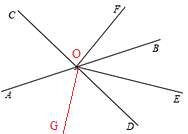
②∵OF⊥CD,
∴∠COF=90°,∠COF+∠EOF+∠EOD=180°,
∵OG⊥OE
∴∠GOE=90°,∠AOG+∠GOE+∠EOB=180°
∵OE平分∠BOD,
∴∠BOE=∠DOE,
∴∠AOG=∠EOF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+5的图象过A(﹣1,0),B(5,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒![]() 个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
(1)求抛物线的表达式;
(2)如图2,当t=1时,若点Q是X轴上的一个动点,如果以Q,P,B为顶点的三角形与△ABC相似,求出Q点的坐标;
(3)如图3,过点P向x轴作垂线分别交x轴,抛物线于E、F两点.
①求PF的长度关于t的函数表达式,并求出PF的长度的最大值;
②连接BF,将△PBF沿BF折叠得到△P′BF,当t为何值时,四边形PFP′B是菱形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).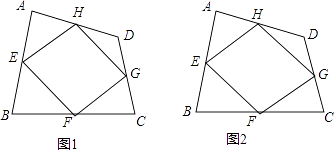
(1)四边形EFGH的形状是 , 证明你的结论.
(2)如图2,请连接四边形ABCD的对角线AC与BD,当AC与BD满足条件时,四边形EFGH是矩形;证明你的结论.
(3)你学过的哪种特殊四边形的中点四边形是矩形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①若a与c相交,b与c相交,则a与b相交;②若a//b,b//c,那么a//c;③经过直线外一点有且只有一条直线与已知直线平行;④两条直线的位置关系有平行与相交.
其中错误的说法有( )
A. 3个B. 2个C. 1个D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店卖出一套衣服,亏损了![]() 元,其中裤子是按
元,其中裤子是按![]() 元卖出的,盈利了
元卖出的,盈利了![]() ;上衣亏损了
;上衣亏损了![]() .求:
.求:
(1)这套衣服中裤子的进价是多少元?
(2)这套衣服中上衣是按多少元卖出的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四个命题
①两条对角线互相平分的四边形是平行四边形;
②两条对角线相等的四边形是矩形;
③两条对角线互相垂直的平行四边形是菱形;
④有一组邻边相等且有一个角是直角的四边形是正方形,
其中是真命题的是( )
A.①②B.③④C.①③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
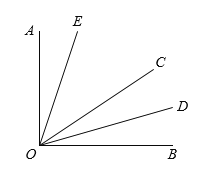
【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠EOC=2∠AOE.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=54°,求∠EOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com