
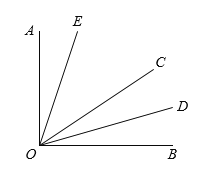
【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠EOC=2∠AOE.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=54°,求∠EOC的度数.
【答案】(1)20°;(2)36°.
【解析】试题分析:设∠AOE=x,则∠EOC=2x,∠AOC=3x,∠COB=90°-3x.根据角平分线定义得到∠COD=∠DOB=45°-1.5x.
(1)根据∠AOD=75°,列方程求解即可;
(2)由∠DOE=∠EOC+∠COD,得到45°+0.5x=54°,解方程即可得到结论.
试题解析:解:设∠AOE=x,则∠EOC=2x,∠AOC=3x,∠COB=90°-3x.∵OD平分∠COB,∴∠COD=∠DOB=![]() ∠COB=45°-1.5x.
∠COB=45°-1.5x.
(1)若∠AOD=75°,即∠AOC+∠COD=75°,则3x+45°-1.5x=75°,解得:x=20°,即∠AOE=20°;
(2)∵∠DOE=∠EOC+∠COD=2x+45°-1.5x=45°+0.5x.若∠DOE=54°,即45°+0.5x=54°,解得:x=18°,则2x=36°,即∠EOC=36°.


科目:初中数学 来源: 题型:
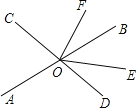
【题目】直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,垂足为O.
(1)若∠EOF=54°,求∠AOC的度数;
(2)①在∠AOD的内部作射线OG⊥OE;
②试探索∠AOG与∠EOF之间有怎样的关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,举行抽奖活动,并规定:顾客每购买100元的商品,就可以随机抽取一张奖券,抽得奖券“紫气东来”、“化开富贵”、“吉星高照”,就可以分别获得100元、50元、20元的购物券,抽得“谢谢惠顾”不赠购物券;如果顾客不愿意抽奖,可以直接获得购物券10元,小明购买了100元的商品,他看到商场公布的前10000张奖券的抽奖结果如下:
奖券种类 | 紫气东来 | 化开富贵 | 吉星高照 | 谢谢惠顾 |
出现张数(张) | 500 | 1000 | 2000 | 6500 |
(1)求“紫气东来”奖券出现的频率;
(2)请你帮助小明判断,抽奖和直接获得购物券,哪种方式更合算?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
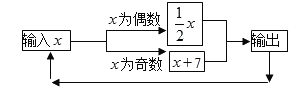
【题目】如图所示的运算程序中,若开始输入的x值为100,我们发现第1次输出的结果为50,第2次输出的结果为25,…,第2018次输出的结果为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2. 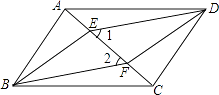
(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF. 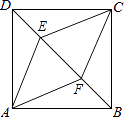
(1)判断四边形AECF是什么特殊四边形,并证明;
(2)若EF=4,DE=BF=2,求四边形AECF的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com