
【题目】如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF. 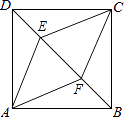
(1)判断四边形AECF是什么特殊四边形,并证明;
(2)若EF=4,DE=BF=2,求四边形AECF的周长.
【答案】
(1)解:四边形AECF是菱形,理由如下:
连接AC,交BD于点O,

∵四边形ABCD是正方形,
∴AC⊥BD,OA=OC=OB=OD
∴DE=BF
∴OE=OF
∴四边形AECF是菱形
(2)解:∵EF=4,DE=BF=2,
∴AC=BD=8,
∴AE= ![]() ,
,
∴四边形AECF的周长为8 ![]()
【解析】(1)连接AC,交BD于点O.利用正方形的性质得出AC⊥BD,OA=OC=OB=OD,进一步得出OE=OF,证得四边形AECF是菱形;(2)利用菱形的性质和勾股定理求得即可.
【考点精析】利用勾股定理的概念和菱形的判定方法对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
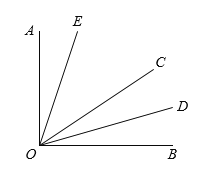
【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠EOC=2∠AOE.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=54°,求∠EOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
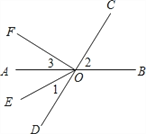
【题目】如图,直线 AB,CD 相交于点O,OE 平分∠AOD,OF⊥OC.
(1)图中∠AOF 的余角是 (把符合条件的角都填出来);
(2)如果∠AOC=130°36′,那么根据 ,可得∠BOD= °;
(3)如果∠1与∠3的度数之比为3:4,求∠EOC和∠2的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种毛巾原零售价为每条6元,凡一次性购买两条以上,商家推出两种优惠销售办法,第一种:“两条按原价,其余按七折付款”;第二种:“全部按原价的八折付款”.若想在购买相同数量的情况下,要使第一种办法比第二种办法得到的优惠多,最少要购买毛巾( )
A. 4条 B. 5条 C. 6条 D. 7条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式: ![]() ,
, ![]() ,给出定义如下:
,给出定义如下:
我们称使等式![]() 成立的一对有理数
成立的一对有理数![]() ,
, ![]() 为“共生有理数对”,记为(
为“共生有理数对”,记为(![]() ,
, ![]() ),如:数对(
),如:数对(![]() ,
, ![]() ),(
),(![]() ,
, ![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)判断数对(![]() ,
, ![]() ),(
),(![]() ,
, ![]() )是不是“共生有理数对”,写出过程;
)是不是“共生有理数对”,写出过程;
(2)若(![]() ,
, ![]() )是“共生有理数对”,求
)是“共生有理数对”,求![]() 的值;
的值;
(3)若(![]() ,
, ![]() )是“共生有理数对”,则(
)是“共生有理数对”,则(![]() ,
, ![]() ) “共生有理数对”(填“是”或“不是”);说明理由;
) “共生有理数对”(填“是”或“不是”);说明理由;
(4)请再写出一对符合条件的 “共生有理数对”为 (注意:不能与题目中已有的“共生有理数对”重复)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为原点,在数轴上点A表示的数为a,点B表示的数为b,且a,b满足|a+2|+(3a+b)2=0.
![]()
(1)a=________,b=_________;
(2)若点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(秒).
①当点P运动到线段OB上,且PO=2PB时,求t的值;
②先取OB的中点E,当点P在线段OE上时,再取AP的中点F,试探究![]() 的值是否为定值?若是,求出该值;若不是,请用含t的代数式表示.
的值是否为定值?若是,求出该值;若不是,请用含t的代数式表示.
③若点P从点A出发,同时,另一动点Q从点B出发,以每秒2个单位长度的速度向左匀速运动,到达点O后立即原速返回向右匀速运动,当PQ=1时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com