
【题目】如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2. 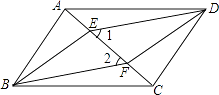
(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
【答案】
(1)证明:如图:
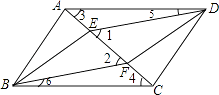
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠3=∠4,
∵∠1=∠3+∠5,∠2=∠4+∠6,∠1=∠2
∴∠5=∠6
∵在△ADE与△CBF中,
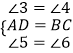
∴△ADE≌△CBF(ASA),
∴AE=CF
(2)证明:∵∠1=∠2,
∴DE∥BF.
又∵由(1)知△ADE≌△CBF,
∴DE=BF,
∴四边形EBFD是平行四边形.
【解析】(1)通过全等三角形△ADE≌△CBF的对应边相等证得AE=CF;(2)根据平行四边形的判定定理:对边平行且相等的四边形是平行四边形证得结论.
【考点精析】本题主要考查了平行四边形的判定与性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】以下四个命题
①两条对角线互相平分的四边形是平行四边形;
②两条对角线相等的四边形是矩形;
③两条对角线互相垂直的平行四边形是菱形;
④有一组邻边相等且有一个角是直角的四边形是正方形,
其中是真命题的是( )
A.①②B.③④C.①③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠EOC=2∠AOE.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=54°,求∠EOC的度数.
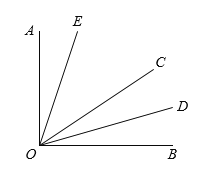
查看答案和解析>>
科目:初中数学 来源: 题型:
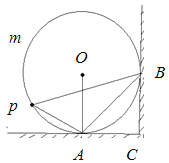
【题目】如图,圆形靠在墙角的截面图,A、B分别为⊙O的切点,BC⊥AC,点P在![]() 上以2°/s的速度由A点向点B运动(A、B点除外),连接AP、BP、BA。
上以2°/s的速度由A点向点B运动(A、B点除外),连接AP、BP、BA。
(1)当∠PBA=28°,求∠OAP的度数;
(2)若点P不在AO的延长线上,请写出∠OAP与∠PBA之间的关系;
(3)当点P运动几秒时,△APB为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,ABCD中,BE,CF分别是∠ABC和∠BCD的一平分线,BE,CF相交于点O. 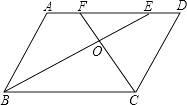
(1)求证:BE⊥CF;
(2)试判断AF与DE有何数量关系,并说明理由;
(3)当△BOC为等腰直角三角形时,四边形ABCD是何特殊四边形?
(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
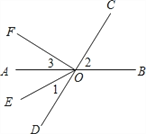
【题目】如图,直线 AB,CD 相交于点O,OE 平分∠AOD,OF⊥OC.
(1)图中∠AOF 的余角是 (把符合条件的角都填出来);
(2)如果∠AOC=130°36′,那么根据 ,可得∠BOD= °;
(3)如果∠1与∠3的度数之比为3:4,求∠EOC和∠2的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com