
【题目】已知,如图,ABCD中,BE,CF分别是∠ABC和∠BCD的一平分线,BE,CF相交于点O. 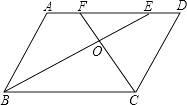
(1)求证:BE⊥CF;
(2)试判断AF与DE有何数量关系,并说明理由;
(3)当△BOC为等腰直角三角形时,四边形ABCD是何特殊四边形?
(直接写出答案)
【答案】
(1)证明:∵四边形ABCD是平行四边形
∴AB∥CD
∴∠ABC+∠BCD=180°
又∵BE,CF分别是∠ABC,∠BCD的平分线
∴∠EBC+∠FCB=90°
∴∠BOC=90°
故BE⊥CF
(2)解:AF=DE
理由如下:
∵AD∥BC
∴∠AEB=∠CBE
又∵BE是∠ABC的平分线,
∴∠ABE=∠CBE
∴∠AEB=∠ABE
∴AB=AE
同理CD=DF
又∵四边形ABCD是平行四边形
∴AB=CD
∴AE=DF
∴AF=DE
(3)解:当△BOC为等腰直角三角形时四边形ABCD是矩形
【解析】(1)平行四边形中邻角互补,且BE、CF分别为一组邻角的平分线,所以BE和CF垂直.(2)在三角形AEB中,因为BE为平分线,AD和BC平行,所以可得∠ABE=∠AEB,即AB=AE,同理,DF=DC,所以AF=DE.(3)当△BOC为等腰直角三角形时,即∠BOC=90°,由题可知,∠ABC=∠BCD=90°,有一个角是直角的平行四边形为矩形.
【考点精析】解答此题的关键在于理解平行四边形的判定与性质的相关知识,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积,以及对矩形的判定方法的理解,了解有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
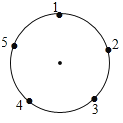
【题目】如图是一个圆,一只电子跳蚤在标有五个数字的点上跳跃,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若跳蚤从2这点开始跳,则经2017次跳后它停在数____对应的点上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2. 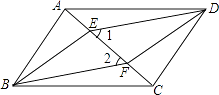
(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE. 
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“61儿童节”举行文具优惠售卖活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.若设铅笔卖出x支,则依题意可列得的一元一次方程为( )
A.1.2×0.8x+2×0.9(60+x)=87
B.1.2×0.8x+2×0.9(60﹣x)=87
C.2×0.9x+1.2×0.8(60+x)=87
D.2×0.9x+1.2×0.8(60﹣x)=87
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com