
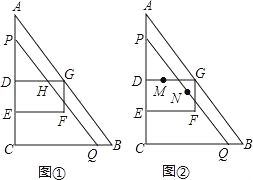
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,点D、E在边AC上,AD=4cm,点E是CD的中点,以DE为边的矩形DEFG的顶点G在边AB上,动点P从点A出发,以1cm/s的速度沿AC向点C运动,过点P作PQ∥AB交BC于点Q,设点P的运动时间为t(s),矩形DEFG与△PCQ重叠部分图形的面积为s(cm2).
(1)在点P的运动过程中,当线段PQ与矩形DEFG的边DG有交点,令交点为H,用含t的代数式表示线段DH的长.
(2)求s与t的函数关系式.
(3)点P出发的同时,动点M从点D出发,以acm/s的速度沿D-G-F-E-F运动,点N是线段PQ中点,在点P的运动过程中,若点M、N能够重合在矩形DEFG的边上,求动点M的速度a.
【答案】(1)3-![]() t,(2)当0<t≤2时,S= 6-
t,(2)当0<t≤2时,S= 6-![]() t2,当2<t≤4时,S=
t2,当2<t≤4时,S= ![]() -
-![]() t,当4<t≤6时,S=
t,当4<t≤6时,S=![]() t2-
t2-![]() t+
t+![]() ,当6<t≤8时,S=0,(3)a=
,当6<t≤8时,S=0,(3)a=![]() 或a=
或a=![]() .
.
【解析】
试题分析:(1)由△ADG∽△ACB求出DG,再由△PDH∽ADG,求出DH,即可;
(2)分四段当0<t≤2时,当2<t≤4时,当4<t≤6时,当6<t≤8时分别求出面积即可;
(3)先判断出,只有点M在EF上时,点P与D重合,M,N才能重合,此时t=4,点M走的路程为at.依题意,由at=8-![]() 或at=8+
或at=8+![]() .
.
试题解析:(1)由运动有,AP=t,AD=4,
∴PD=4-t,
∵△ADG∽△ACB,
∴![]() ,
,
∴DG=3,
∵△PDH∽ADG,
∴![]() ,
,
∴![]() ,
,
∴DH=![]() (4-t)=3-
(4-t)=3-![]() t,
t,
(2)当0<t≤2时,如图1,

S=S四边形DEFG-S△GFH=3×2-![]() t×
t×![]() t=6-
t=6-![]() t2,
t2,
当2<t≤4时,如图2,

S=S四边形DEFG=![]() ×2[
×2[![]() (4-t)+
(4-t)+![]() (6-t)]=
(6-t)]=![]() -
-![]() t,
t,
当4<t≤6时,如图3,
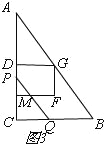
S=S△GFH=![]() ×(6-t)×
×(6-t)×![]() (6-t)=
(6-t)=![]() t2-
t2-![]() t+
t+![]() ,
,
当6<t≤8时,S=0,
(3)由题意知,只有点M在EF上时,点P与D重合,M,N才能重合,此时t=4,
点M走的路程为at.依题意,由at=8-![]() 或at=8+
或at=8+![]() ,
,
∴a=![]() 或a=
或a=![]() .
.


科目:初中数学 来源: 题型:
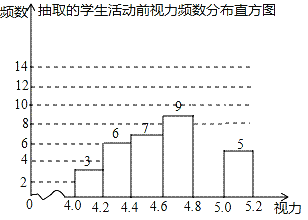
【题目】为了保护视力,学校计划开展“爱眼护眼”视力保健活动,为使活动更具有实效性,先对学生视力情况进行调查,随机抽取40名学生,检查他们的视力,并绘制不完整的直方图(数据包括左端点不包括右端点,精确到0.1),请结合直方图的信息解答下列问题:
(1)统计图中,4.8≤x<5.0的学生数是 人;
(2)将频数分布直方图补充完整;
(3)若绘制“学生视力扇形统计图”,视力达到4.8及以上为达标,则视为达标学生所对应扇形的圆心角度数为 °;
(4)若全校共有800名学生,则视力达标的学生估计有 名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,李明在自家楼房的窗口A处,测量楼前的路灯CD的高度,现测得窗口处A到路灯顶部C的仰角为44°,到地面的距离AB为20米,楼底到路灯的距离BD为12米,求路灯CD的高度(结果精确到0.1)
【参考数据:sin44°=0.69,cos44°=0.72,tan44°=0.97】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长度为2cm、3cm、4cm、5cm的四条线段,若以其中的三条线段为边构成三角形,可以构成不同的三角形共有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com