Question

【题目】如图，在△ABC中，分别以AC，BC为边作等边△ACD和等边△BCE.设△ACD，△BCE，△ABC的面积分别是S1，S2，S3，现有如下结论：

①S1∶S2＝AC2∶BC2；②连接AE，BD，则△BCD≌△ECA；③若AC⊥BC，则S1·S2＝S23.

其中结论正确的序号是__________.

Answer 1

【答案】①②③

【解析】

①根据相似三角形面积的比等于相似比的平方判断；

②根据SAS即可求得全等；

③根据面积公式即可判断．

①S1：S2=AC2：BC2正确，

∵△ADC与△BCE是等边三角形，

∴△ADC∽△BCE，

∴S1：S2=AC2：BC2．

②△BCD≌△ECA正确，

∵△ADC与△BCE是等边三角形，

∴∠ACD=∠BCE=60°

∴∠ACD+∠ACB=∠BCE+∠ACD，

即∠ACE=∠DCB，

在△ACE与△DCB中，

，

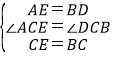∴△BCD≌△ECA（SAS）．

③若AC⊥BC，则S1S2=S32正确，

设等边三角形ADC的边长=a，等边三角形BCE边长=b，则△ADC的高=a，△BCE的高=b，

∴S1=aa=a2，S2=bb=b2，

∴S1S2=a2b2=a2b2，

∵S3=ab，

∴S32=a2b2，

∴S1S2=S32．