
【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于点B和A,与反比例函数的图像交于C、D,CE⊥x轴于点E,若![]() ,OB=4,OE=2,点D的坐标为(6,m).
,OB=4,OE=2,点D的坐标为(6,m).
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积。

【答案】(1)直线AB的解析式是:y=12x+2,反比例函数的解析式是:y=![]() ;
;
(2)S△COD= 8.
【解析】试题分析:(1)根据已知条件求出A、B、C点坐标,用待定系数法求出直线AB和反比例的函数解析式;
(2)联立一次函数的解析式和反比例的函数解析式可得交点D的坐标,从而根据三角形面积公式求解.
试题解析:(1)∵OB=4,OE=2,
∴BE=2+4=6.
∵CE⊥x轴于点E, tan∠ABO=![]() =
=![]() .
.
∴OA=2,CE=3.
∴点A的坐标为(0,2)、点B的坐标为(4,0)、点C的坐标为(2,3).
设直线AB的解析式为y=kx+b,
则![]() ,
,
解得: 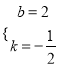 .
.
故直线AB的解析式为y=![]() x+2.
x+2.
设反比例函数的解析式为y=![]() .
.
将点C的坐标代入,得3=![]() ,
,
∴m=6.
∴该反比例函数的解析式为y= ![]() .
.
(2)联立反比例函数的解析式和直线AB的解析式可得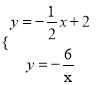 ,
,
可得交点D的坐标为(6,1),
则△BOD的面积=4×1÷2=2,
△BOC的面积=4×3÷2=6,
故△OCD的面积为2+6=8.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
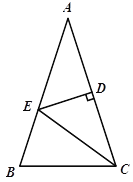
【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=12,求BC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.有一个内角是锐角的三角形是锐角三角形B.钝角三角形的三个内角都是钝角
C.有一个内角是直角的三角形是直角三角形D.三条边都相等的三角形称为等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体纸箱的长、宽、高分别为50cm、30cm、60cm,一只蚂蚁从点A处沿着纸箱的表面爬到点B处.蚂蚁爬行的最短路程为_______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=30°,D为BC上一点,且∠DAB=45°.
(1) 求∠DAC的度数.
(2) 求证:△ACD是等腰三角形.
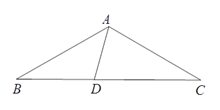
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在社会实践活动中,某中学对甲、乙,丙、丁四个超市三月份的苹果价格进行调查.它们的价格的平均值均为3.50元,方差分别为S甲2=0.3,S乙2=0.4,S丙2=0.1,S丁2=0.25.三月份苹果价格最稳定的超市是( )
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
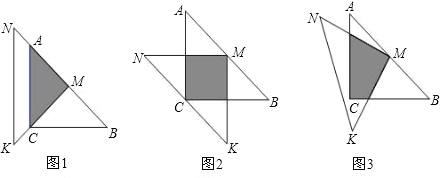
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 ,周长为 .
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 ,周长为 .
2(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com