
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,在⊙O的切线CM上取一点P,使得∠CPB=∠COA.
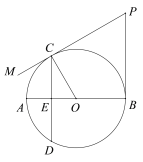
(1)求证:PB是⊙O的切线;
(2)若CD=6,∠AOC=60°,求PB的长.
【答案】(1)详见解析;(2)6
【解析】
(1)根据切线的性质和四边形的内角和即可得出∠PBO=90°,进而证得结论;
(2)解法1:连接OP,先根据垂径定理和30°的直角三角形的性质求出半径OC的长,即为OB的长,再利用四边形的内角和和切线长定理求出∠BPO的度数,进一步即可求出PB的长;
解法2:连接BC,先证明△PBC是等边三角形,再在直角△BCE中求出BC的长即可.
(1)证明: ∵ PC与⊙O相切于点C,∴ OC⊥PC,∴ ∠OCP=90°.
∵ ∠AOC=∠CPB,∠AOC+∠BOC=180°,
∴ ∠BOC+∠CPB=180°.
在四边形PBOC中,∠PBO=360°-∠CPB-∠BOC-∠PCO=90°.
∴ 半径OB⊥PB,∴ PB是⊙O的切线;
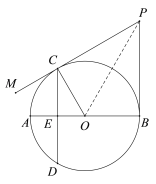
(2)解法1:连接OP,如图.
∵∠AOC=60°,∴∠BOC=120°.
∵ ∠OCP=∠OBP=90°,∴∠BPC=360°-120°-2×90°=60°.
∵ PB,PC都是⊙O的切线,∴ PO平分∠BPC,∴∠CPO=∠BPO=30°.
∵CD⊥AB,AB是⊙O的直径,CD=6,∴![]() ,
,
∵∠AOC=60°,CD⊥AB,∴∠ACO=30°,![]() =OB.
=OB.
∴PB= OB·![]() =
=![]() ·
·![]() = 6.
= 6.
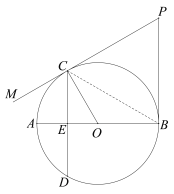
解法2:连接BC,如图.
∵∠AOC=60°,∴∠BOC=120°,
∵ ∠OCP=∠OBP=90°,∴∠BPC=360°-120°-2×90°=60°,
∵ PB,PC都是⊙O的切线,∴ PB=PC,
∴ △PBC为等边三角形,∴PB=BC.
∵CD⊥AB,AB是⊙O的直径,CD=6,∴![]() ,
,
∵∠AOC=60°,CD⊥AB,∴∠ABC=30°,
∴BC=2CE=6,∴PB= BC= 6.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0 (a≠0)有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,方程x2-6x+8=0的两个根是2和4,则方程x2-6x+8=0就是“倍根方程”.
(1)若一元二次方程x2-3x+c=0是“倍根方程”,则c= ;
(2)若(x-2) (mx-n)=0(m≠0)是“倍根方程”,求代数式4m2-5mn+n2的值;
(3)若方程ax2+bx+c=0 (a≠0)是倍根方程,且相异两点M(1+t,s),N(4-t,s),都在抛物线y=ax2+bx+c上,求一元二次方程ax2+bx+c=0 (a≠0)的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则![]() 的最小值为________.
的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若存在过点P的直线l交⊙C于异于点P的A,B两点,在P,A,B三点中,位于中间的点恰为以另外两点为端点的线段的中点时,则称点P为⊙C 的相邻点,直线l为⊙C关于点P的相邻线.
(1)当⊙O的半径为1时,
①分别判断在点D(![]() ,
, ![]() ),E(0,﹣
),E(0,﹣![]() ),F(4,0)中,是⊙O的相邻点有 ;
),F(4,0)中,是⊙O的相邻点有 ;
②请从①中的答案中,任选一个相邻点,在图1中做出⊙O关于它的一条相邻线,并说明你的作图过程;
③点P与点O的距离d满足范围___________________时,点P是⊙O的相邻点;
④点P在直线y=﹣x+3上,若点P为⊙O的相邻点,求点P横坐标x的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标x的取值范围.
与x轴,y轴分别交于点M,N,若线段MN上存在⊙C的相邻点P,直接写出圆心C的横坐标x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为3cm,点N在AC边上,AN=1cm.△ABC边上的动点M从点A出发,沿A→B→C运动,到达点C时停止.设点M运动的路程为xcm,MN的长为ycm.
小西根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小西的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了y与x的几组对应值;
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
y/cm | 1 | 0.87 | 1 | 1.32 | 2.18 | 2.65 | 2.29 | 1.8 | 1.73 | 1.8 | 2 |
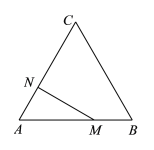
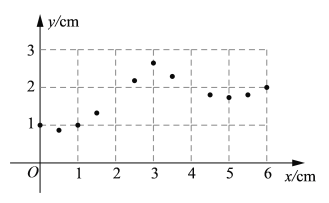
(2)在平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点,画出该函数的图象;
中,描出补全后的表中各组数值所对应的点,画出该函数的图象;
(3) 结合函数图象,解决问题:当MN=2cm时,点M运动的路程为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在矩形![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点,
上一点,![]() ,连接
,连接![]() ,
,![]() . 动点
. 动点![]() 以每秒1个单位的速度从点
以每秒1个单位的速度从点![]() 出发沿
出发沿![]() 向终点
向终点![]() 运动,同时动点
运动,同时动点![]() 以每秒2个单位的速度从点
以每秒2个单位的速度从点![]() 出发沿
出发沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
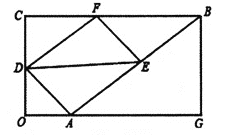
(1)求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)求证:四边形![]() 为平行四边形;
为平行四边形;
(3)探索当![]() 为何值时,
为何值时,![]() 与以
与以![]() ,
,![]() ,
,![]() 为顶点的三角形相似?
为顶点的三角形相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,![]() )三点.
)三点.

(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com