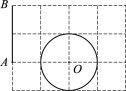
【题目】如图所示的网格是正方形网格，线段AB绕点A顺时针旋转α（0°＜α＜180°）后与⊙O相切，则α的值为_____．
【答案】60°或120 °
【解析】
线段AB绕点A顺时针旋转α（0°＜α＜180°）后与⊙O相切，切点为C′和C″，连接OC′、OC″，根据切线的性质得OC′⊥AB′，OC″⊥AB″，利用直角三角形30度的判定或三角函数求出∠OAC′=30°，从而得到∠BAB′=60°，同理可得∠OAC″=30°，则∠BAB″=120°．
线段AB绕点A顺时针旋转α（0°＜α＜180°）后与⊙O相切，切点为C′和C″，连接OC′、OC″，
则OC′⊥AB′，OC″⊥AB″，
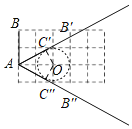
在Rt△OAC′中，∵OC′=1，OA=2，
∴∠OAC′=30°，
∴∠BAB′=60°，
同理可得∠OAC″=30°，
∴∠BAB″=120°，
综上所述，α的值为60°或120°．
故答案为60°或120°．
科目：初中数学 来源： 题型：
【题目】如图所示，某幼儿园为了加强安全管理，决定将园内的滑滑板的倾斜角由45°降为30°，已知原滑滑板AB的长为5米，点D、B、C在同一水平地面上.若滑滑板的正前方能有3米长的空地就能保证安全，原滑滑板的前方有6米长的空地，像这样改造是否可行？请说明理由.（参考数据：
≈1.414，
≈1.732，
≈2.449）
查看答案和解析>>
科目：初中数学 来源： 题型：
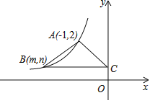
【题目】如图，在平面直角坐标系中，函数
(x<0，常数k<0)的图象经过点A(-1，2)，B(m，n)且(m<-1)，过点B作y轴的垂线，垂足为C，若△ABC面积为2，求点B的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（12分）阅读理解：
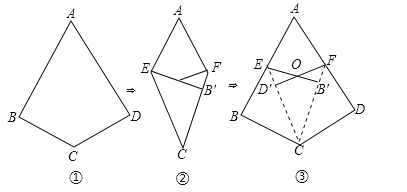
如图①，如果四边形ABCD满足AB=AD，CB=CD，∠B=∠D=90°，那么我们把这样的四边形叫做“完美筝形”．
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状，再展开得到图③，其中CE，CF为折痕，∠BCE=∠ECF=∠FCD，点B′为点B的对应点，点D′为点D的对应点，连接EB′，FD′相交于点O．
简单应用：
（1）在平行四边形、矩形、菱形、正方形四种图形中，一定为“完美筝形”的是 ；
（2）当图③中的∠BCD=120°时，∠AEB′= °；
（3）当图②中的四边形AECF为菱形时，对应图③中的“完美筝形”有 个（包含四边形ABCD）．
拓展提升：
（4）当图③中的∠BCD=90°时，连接AB′，请探求∠AB′E的度数，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数学课上学习了圆周角的概念和性质：“顶点在圆上，两边与圆相交”，“同弧所对的圆周角相等”，小明在课后继续对圆外角和圆内角进行了探究．
下面是他的探究过程，请补充完整：
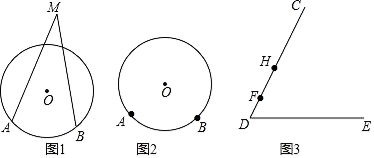
定义概念：顶点在圆外，两边与圆相交的角叫做圆外角，顶点在圆内，两边与圆相交的角叫做圆内角．如图1，∠M为
所对的一个圆外角．
(1)请在图2中画出所对的一个圆内角；
提出猜想
(2)通过多次画图、测量，获得了两个猜想：一条弧所对的圆外角______这条弧所对的圆周角；一条弧所对的圆内角______这条弧所对的圆周角；(填“大于”、“等于”或“小于”)
推理证明：
(3)利用图1或图2，在以上两个猜想中任选一个进行证明；
问题解决
经过证明后，上述两个猜想都是正确的，继续探究发现，还可以解决下面的问题．
(4)如图3，F，H是∠CDE的边DC上两点，在边DE上找一点P使得∠FPH最大．请简述如何确定点P的位置．(写出思路即可，不要求写出作法和画图)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，点P和图形W的中间点的定义如下：Q是图形W上一点，若M为线段PQ的中点，则称M为点P和图形W的中间点．C（-2，3），D（1，3），E（1，0），F（-2，0）
（1）点A（2,0），
①点A和原点的中间点的坐标为 ；
②求点A和线段CD的中间点的横坐标m的取值范围；
（2）点B为直线y=2x上一点，在四边形CDEF的边上存在点B和四边形CDEF的中间点，直接写出点B的横坐标n的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
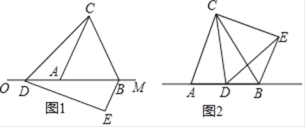
【题目】已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE．
（1）如图1，求证：△CDE是等边三角形．
（2）设OD＝t，
①当6＜t＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE周长的最小值；若不存在，请说明理由．
②求t为何值时，△DEB是直角三角形（直接写出结果即可）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：A（0，3），B（3，0），C（3，4）三点，点P（x，﹣0.5x），当△ABP的面积等于△ABC的面积时，则P点的坐标是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
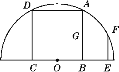
【题目】如图，两正方形彼此相邻，且大正方形ABCD的顶点A，D在半圆O上，顶点B，C在半圆O的直径上；小正方形BEFG的顶点F在半圆O上，E点在半圆O的直径上，点G在大正方形的边AB上．若小正方形的边长为4 cm，求该半圆的半径．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com