
����Ŀ����ѧ����ѧϰ��Բ�ܽǵĸ�������ʣ���������Բ�ϣ�������Բ�ཻ������ͬ�����Ե�Բ�ܽ��������С���ڿκ������Բ��Ǻ�Բ�ڽǽ�����̽����
����������̽�����̣��벹��������
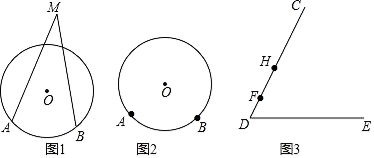
������������Բ�⣬������Բ�ཻ�Ľǽ���Բ��ǣ�������Բ�ڣ�������Բ�ཻ�Ľǽ���Բ�ڽǣ���ͼ1����MΪ![]() ���Ե�һ��Բ��ǣ�
���Ե�һ��Բ��ǣ�
(1)����ͼ2�л���![]() ���Ե�һ��Բ�ڽǣ�
���Ե�һ��Բ�ڽǣ�
�������
(2)ͨ����λ�ͼ��������������������룺һ�������Ե�Բ���______���������Ե�Բ�ܽǣ�һ�������Ե�Բ�ڽ�______���������Ե�Բ�ܽǣ�(������������������������С����)
����֤����
(3)����ͼ1��ͼ2��������������������ѡһ������֤����
������
����֤���������������붼����ȷ�ģ�����̽�����֣������Խ����������⣮
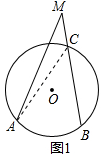
(4)��ͼ3��F��H�ǡ�CDE�ı�DC�����㣬�ڱ�DE����һ��Pʹ�á�FPH�����������ȷ����P��λ�ã�(д��˼·���ɣ���Ҫ��д�������ͻ�ͼ)
���𰸡���1����������2��С�ڣ����ڣ�3����������4��������
��������
��1���ڡ�O����ȡһ��M������AM��BM��
��2���۲�ͼ�Σ���֪��һ�������Ե�Բ���С�����������Ե�Բ�ܽǣ�һ�������Ե�Բ�ڽǴ������������Ե�Բ�ܽǣ����ʵý⣻
��3����i��BM���O�ཻ�ڵ�C������AC��������������ǵ����ʿɵó���ACB=��M+��MAC��������֤����ACB����M����ii���ӳ�BM����O�ڵ�C������AC��������������ǵ����ʿɵó���AMB=��ACB+��CAM��������֤����AMB����ACB��
��4���ɣ�2���Ľ��ۣ���֪��������F��H��Բ��DE����ʱ���е㼴Ϊ����ĵ�P��
��1����ͼ2��ʾ��
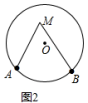
��2���۲�ͼ�Σ���֪��һ�������Ե�Բ���С�����������Ե�Բ�ܽǣ�һ�������Ե�Բ�ڽǴ������������Ե�Բ�ܽǣ�
�ʴ�Ϊ��С�ڣ����ڣ�
��3��֤������i����ͼ1��BM���O�ཻ�ڵ�C������AC��
�ߡ�ACB����M+��MAC��
���ACB����M��
��ii����ͼ4���ӳ�BM����O�ڵ�C������AC��
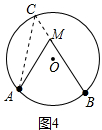
�ߡ�AMB����ACB+��CAM��
���AMB����ACB��
��4����ͼ3��������F��H��Բ��DE����ʱ���е㼴Ϊ����ĵ�P��


 һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O������Rt��ABC����P����Q�ֱ���ֱ�DZ�BC��б��AB�ϣ�PQ��AB����PQ���O���У���AC��2PQ����tan��B��ֵΪ��������
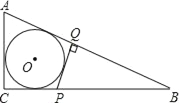
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
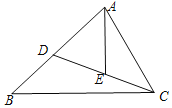
����Ŀ����֪����ͼ������ABC�У���D�ڱ�AB�ϣ���E���߶�CD�ϣ��ҡ�ACD=��B=��BAE.
��1����֤��![]() ��
��
��2������EΪCD�е�ʱ����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
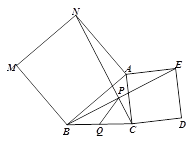
����Ŀ��̽������ͼ���ֱ��ԡ�ABC������AB��ACΪ��������������ABMN��������ACDE��CN��BE���ڵ�P. ��֤����ANC = ��ABE.
Ӧ�ã�Q���߶�BC���е㣬����PQ. ��BC = 6����PQ = ___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC����OB���ۣ�ʹ��A���ڵ�A'������B������(8��4)�����A'��������( )
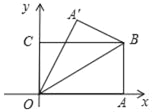
A. (4��![]() ) B. (
) B. (![]() ��
��![]() )
)
C. (![]() ��
��![]() ) D. (
) D. (![]() ��
��![]() )
)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������������������߶�AB�Ƶ�A˳ʱ����ת����0��������180���������O���У�������ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪���κ���y=mx2+3mx��![]() m��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ������D�͵�B���ڹ���A��ֱ��l��y=��
m��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ������D�͵�B���ڹ���A��ֱ��l��y=��![]() x��
x��![]() �Գƣ�
�Գƣ�
��1����A��B��������꼰���κ�������ʽ��
��2����ͼ2����ֱ��AD������B��AD��ƽ���߽�ֱ��1�ڵ�E������P��ֱ��AD�ϵ�һ���㣬��Q��ֱ��AE�ϵ�һ���㣮����DQ��QP��PE������DQ+QP+PE����Сֵ���������ڣ���˵�����ɣ�
��3�������κ���ͼ������ƽ��![]() ����λ��������ƽ��3
����λ��������ƽ��3![]() ����λ��ƽ�ƺ�Ķ��κ���ͼ���ϴ���һ��M���������Ϊ3����y�����Ƿ���ڵ�F��ʹ�á�MAF=45���������ڣ��������F���ꣻ�������ڣ���˵�����ɣ�
����λ��ƽ�ƺ�Ķ��κ���ͼ���ϴ���һ��M���������Ϊ3����y�����Ƿ���ڵ�F��ʹ�á�MAF=45���������ڣ��������F���ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������������y= ![]() ��ͼ����һ�κ���y=x+b��ͼ��
��ͼ����һ�κ���y=x+b��ͼ��
�ڵ�A��1��4������B��-4��n����

��1����һ�κ����ͷ����������Ľ���ʽ��
��2�����OAB�������
��3��ֱ��д��һ�κ���ֵ���ڷ���������ֵ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ���.
��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ���.
��1����A��B��C�����ꣻ
��2����MΪ�߶�AB��һ�㣨��M�����A��B�غϣ�������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N.����P�ڵ�Q��ߣ�������PQMN���ܳ����ʱ������AEM�������
��3���ڣ�2���������£�������PMNQ���ܳ����ʱ������DQ.����������һ��F��y���ƽ���ߣ���ֱ��AC���ڵ�G����G�ڵ�F���Ϸ���.��FG=![]() DQ�����F������.
DQ�����F������.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com