
【题目】阅读下列材料,并完成相应的任务.
我们知道,二元一次方程有无数个解.在平面直角坐标系中,我们标出以这个方程的解为坐标的点,就会发现这些点在同一条直线上.例如:![]() ,方程x﹣y=﹣1的一个解,对应点为(1,2).
,方程x﹣y=﹣1的一个解,对应点为(1,2).
我们在平面直角坐标系中标出,另外方程x﹣y=﹣1的解还对应点(2,3),(3,4)…将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程x﹣1=﹣1的解,所以,我们就把这条直线叫做方程x﹣y=﹣1的图象.
一般的,任意二元一次方程解的对应点连成的直线就叫这个方程的图象.那么每个二元一次方程组应该对应两条直线,解这个方程组,相当于确定两条直线交点的坐标.
(1)已知A(1,1),B(﹣3,4),C(,2),则点 (填“A”、”B”、“C”)在方程2x﹣y=﹣1的图象上;
(2)求方程2x+3y=9和方程3x﹣4y=5图象的交点坐标.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某小区改善生态环境,实行生活垃圾的分类处理,将生活垃圾分成三类:厨房垃圾、可回收垃圾和其他垃圾,分别记为m,n,p,并且设置了相应的垃圾箱,“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率;
(2)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共1 000吨生活垃圾,数据统计如下(单位:吨):
A | B | C | |
m | 400 | 100 | 100 |
n | 30 | 240 | 30 |
p | 20 | 20 | 60 |
请根据以上信息,试估计“厨房垃圾”投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,作斜边AB上中线CD,得到第1个三角形ACD;
,作斜边AB上中线CD,得到第1个三角形ACD;![]() 于点E,作
于点E,作![]() 斜边DB上中线EF,得到第2个三角形DEF;依次作下去
斜边DB上中线EF,得到第2个三角形DEF;依次作下去![]() 则第1个三角形的面积等于______,第n个三角形的面积等于______.
则第1个三角形的面积等于______,第n个三角形的面积等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,D、E是BC边上的点,连接AD、AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′.
(1)求证:△ABD≌△ACD′;
(2)如图2,若∠BAC=120°,探索BD,DE,CE之间满足怎样的数量关系时,△CD′E是正三角形;
(3)如图3,若∠BAC=90°,求证:DE2=BD2+EC2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
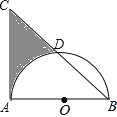
A. 16 B. 24-4π C. 32-4π D. 32-8π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料(1),并利用(1)的结论解决问题(2)和问题(3).
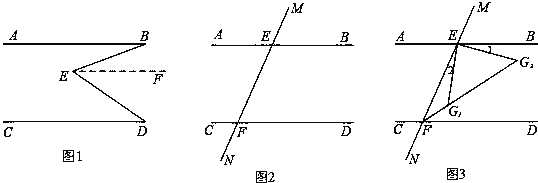
(1)如图1,AB∥CD,E为形内一点,连结BE、DE得到∠BED,求证:∠E=∠B+∠D
悦悦是这样做的:
过点E作EF∥AB.则有∠BEF=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
∴∠BEF+∠FED=∠B+∠D.
即∠BED=∠B+∠D.
(2)如图2,画出∠BEF和∠EFD的平分线,两线交于点G,猜想∠G的度数,并证明你的猜想.
(3)如图3,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1和G2,求证:∠FG1E+∠G2=180°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形![]() 的底边
的底边![]() 长为
长为![]() ,面积是
,面积是![]() , 腰
, 腰![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 边于
边于![]() 点.若点
点.若点![]() 为
为![]() 边的中点,点
边的中点,点![]() 为线段EF上一动点,则
为线段EF上一动点,则![]() 周长的最小值为( )
周长的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com