
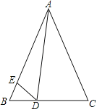
【题目】如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.
(1)求证:△BDE∽△CAD;
(2)求证:△ADE∽△ABD.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
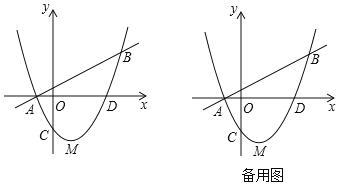
【题目】如图已知直线![]() 与抛物线y=ax2+bx+c相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,﹣
与抛物线y=ax2+bx+c相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,﹣![]() ),交x轴正半轴于D点,抛物线的顶点为M.
),交x轴正半轴于D点,抛物线的顶点为M.
(1)求抛物线的解析式;
(2)设点P为直线AB下方的抛物线上一动点,当△PAB的面积最大时,求△PAB的面积及点P的坐标;
(3)若点Q为x轴上一动点,点N在抛物线上且位于其对称轴右侧,当△QMN与△MAD相似时,求N点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与
与 ![]() 轴交于
轴交于![]() 和
和![]() ,与
,与 ![]() 轴交于
轴交于 ![]() 点,点
点,点![]() 关于抛物线的对称轴的对称点为点
关于抛物线的对称轴的对称点为点![]() .
.
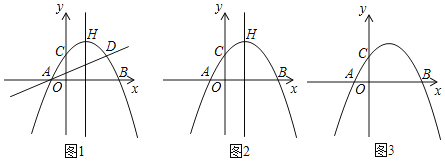
(1)求此抛物线的解析式和对称轴.
(2)如图 2,当点![]() 在抛物线的对称轴上运动时,在直线
在抛物线的对称轴上运动时,在直线![]() 上是否存在点
上是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,请求出点
为顶点的四边形为平行四边形?若存在,请求出点 ![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)如图 3,当点![]() 、
、![]() 、
、![]() 三点共圆时,请求出该圆圆心的坐标.
三点共圆时,请求出该圆圆心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
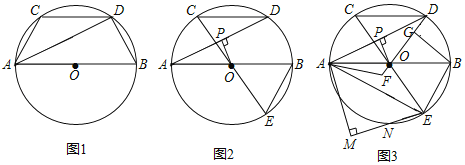
【题目】如图,在⊙O中,AB是⊙O的直径,CD∥AB,
(1)如图1,证明:AC=BD;
(2)如图2,连接CO并延长交⊙O于点E,OP⊥AD,垂足为P,证明:BE=2OP;
(3)如图3,在(2)的条件下,连接DO,点F为DO延长线上一点,若∠AFO+∠ABE=180°,过点B作BG⊥OD,垂足为G,点N为![]() 上一点,AM⊥EN,垂足为M,若GF=4,OP=
上一点,AM⊥EN,垂足为M,若GF=4,OP=![]() ,AM=2NE,求AM的长.
,AM=2NE,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2017年张学友演唱会”于6月3日在我市关山湖奥体中心举办,小张去离家2520米的奥体中心看演唱会,到奥体中心后,发现演唱会门票忘带了,此时离演唱会开始还有23分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回奥体中心,已知小张骑车的时间比跑步的时间少用了4分钟,且骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小张跑步的平均速度;
(2)如果小张在家取票和寻找“共享单车”共用了5分钟,他能否在演唱会开始前赶到奥体中心?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
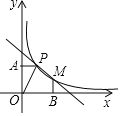
【题目】如图,已知反比例函数![]() 的图象和一次函数
的图象和一次函数![]() 的图象都过点
的图象都过点![]() ,过点P作y轴的垂线,垂足为A,O为坐标原点,
,过点P作y轴的垂线,垂足为A,O为坐标原点,![]() 的面积为1.
的面积为1.
(1)求反比例函数和一次函数的解析式;
(2)设反比例函数图象与一次函数图象的另一交点为M,过M作x轴的垂线,垂足为B,求五边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
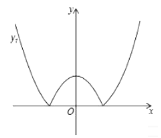
【题目】如图,将二次函数![]() (其中
(其中![]() )的图象在
)的图象在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,图象的其余部分保持不变,形成新的图象记为
轴翻折,图象的其余部分保持不变,形成新的图象记为![]() ,另有一次函数
,另有一次函数![]() 的图象记为
的图象记为![]() ,若
,若![]() 与
与![]() 恰有两个交点时,则
恰有两个交点时,则![]() 的范围是________.
的范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com