
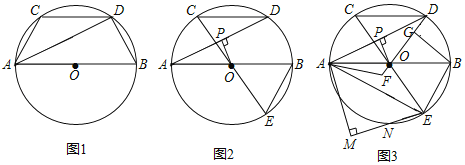
【题目】如图,在⊙O中,AB是⊙O的直径,CD∥AB,
(1)如图1,证明:AC=BD;
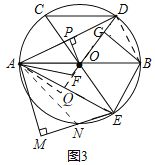
(2)如图2,连接CO并延长交⊙O于点E,OP⊥AD,垂足为P,证明:BE=2OP;
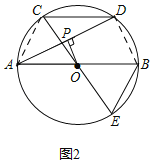
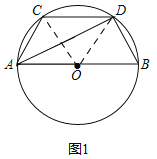
(3)如图3,在(2)的条件下,连接DO,点F为DO延长线上一点,若∠AFO+∠ABE=180°,过点B作BG⊥OD,垂足为G,点N为![]() 上一点,AM⊥EN,垂足为M,若GF=4,OP=
上一点,AM⊥EN,垂足为M,若GF=4,OP=![]() ,AM=2NE,求AM的长.
,AM=2NE,求AM的长.
【答案】(1)详见解析;(2)详见解析;(3)2![]() .
.
【解析】
(1)先判断出∠ADC=∠BAD,进而判断出∠AOC=∠BOD,即可得出结论;
(2)先判断出OP∥BD,进而得出BD=2OP,再判断出BE=BD,即可得出结论;
(3)先判断出△BOG≌△AOQ(AAS),得出BG=AQ,OG=OQ=4﹣x,进而FQ=OQ﹣OF=4﹣2x,再判断出△BDG≌△AFQ(AAS),得出DG=FQ=4﹣2x,得出OB=OD=OG+DG=8﹣3x,进而求出x的值,利用勾股定理求出AE,再判断出△AMN∽△AEB,进而得出![]() ,进而判断出AM=2MN,得出AM=ME,即可得出结论.
,进而判断出AM=2MN,得出AM=ME,即可得出结论.
证明:(1)如图1,连接OC,OD,
∵CD∥AB,
∴∠ADC=∠BAD,
∵∠AOC=2∠ADC,∠BOD=2∠BAD,
∴∠AOC=∠BOD,
∴AC=BD;
(2)如图2,连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵OP⊥AD,
∴∠APO=90°=∠ADB,
∴OP∥BD,
∵OA=OB=![]() AB,
AB,
∴BD=2OP,
∵∠AOC=∠BOE,
∴AC=BE,
由(1)知,AC=BD,
∴BE=BD,
∴BE=2OP;
(3)如图3,设OF=x,则OG=FG﹣OF=4﹣x,
过点A作AQ⊥DF,交DF的延长线于Q,
∵BG⊥DF,
∴∠BGO=∠AQO=90°,
∵∠BOG=∠AOQ,OA=OB,
∴△BOG≌△AOQ(AAS),
∴BG=AQ,OG=OQ=4﹣x,
∴FQ=OQ﹣OF=4﹣2x,
由(2)知,BE=BD,
∴∠BOD=∠BOE,
∵OB=OD=OE,
∴∠ODB=∠OBD=∠ABE=∠OEB,
∵∠AFO+∠AFQ=180°,∠AFO+∠ABE=180°,
∴∠AFQ=∠ABE,
∴∠AFQ=∠ODB,
∵BG=AQ,
∴△BDG≌△AFQ(AAS),
∴DG=FQ=4﹣2x,
∴OB=OD=OG+DG=8﹣3x,
在Rt△BGO中,根据勾股定理得,BG2=OB2﹣OG2=(8﹣3x)2﹣(4﹣x)2,
∵OP=![]() ,
,
∴BD=BE=2OP=2![]() ,
,
在Rt△BGD中,根据勾股定理得,BG2=BD2﹣DG2=(2![]() )2﹣(4﹣2x)2,
)2﹣(4﹣2x)2,
∴(8﹣3x)2﹣(4﹣x)2=20﹣(4﹣2x)2,
∴x=1或x=![]() (此时,OQ=OG=
(此时,OQ=OG=![]() <OF,而∠ABE是锐角,所以,∠AFO是钝角,所以,OQ>OF,相互矛盾,舍去),
<OF,而∠ABE是锐角,所以,∠AFO是钝角,所以,OQ>OF,相互矛盾,舍去),
∴OB=OD=5,
∴AB=10,
由(2)知,BE=BD=2![]() ,
,
在Rt△ABE中,根据勾股定理得,AE=![]() =4
=4![]() ,
,
连接AN,
四边形ANEB是圆内接四边形,
∴∠ANM=∠ABE,
∵AM⊥ME,
∴∠AMN=90°=∠AEB,
∴△AMN∽△AEB,
∴![]() =
=![]() =
=![]() ,
,
设AM=2a,AN=![]() a,根据勾股定理得,MN=
a,根据勾股定理得,MN=![]() =a,
=a,
∵AM=2NE=2a,
∴NE=a,
∴ME=MN+NE=2a,
∴AM=AN,
根据勾股定理得,AE2=2AM2,
∴AM=![]() =2
=2![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 5 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
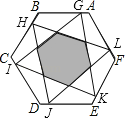
【题目】如图,已知正六边形ABCDEF的边长为![]() ,点G,H,I,J,K,L依次在正六边形的六条边上,且AG=BH=CI=DJ=EK=FL,顺次连结G,I,K,和H,J,L,则图中阴影部分的周长C的取值范围为( )
,点G,H,I,J,K,L依次在正六边形的六条边上,且AG=BH=CI=DJ=EK=FL,顺次连结G,I,K,和H,J,L,则图中阴影部分的周长C的取值范围为( )
A.6≤C≤6![]() B.3≤C≤3
B.3≤C≤3![]() C.3
C.3![]() ≤C≤6D.3
≤C≤6D.3![]() ≤C≤6
≤C≤6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的两个实数根.
=0的两个实数根.
(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图:


请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小张同学共调查了_____名居民的年龄,扇形统计图中a=_____;
(2)补全条形统计图,并注明人数;
(3)若在该辖区中随机抽取一人,那么这个人年龄是60岁及以上的概率为_____;
(4)若该辖区年龄在0~14岁的居民约有3500人,请估计该辖区居民人数是_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
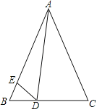
【题目】如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.
(1)求证:△BDE∽△CAD;
(2)求证:△ADE∽△ABD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是平面内不与点
是平面内不与点![]() 重合的任意一点,连接
重合的任意一点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点.
的中点.
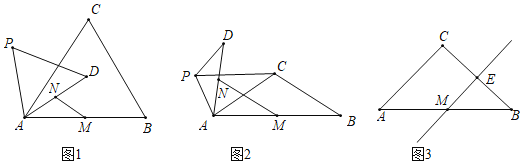
(1)问题发现:
如图1,当![]() 时,
时,![]() 的值是_________,直线
的值是_________,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是________.
相交所成的较小角的度数是________.
(2)类比探究:
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的较小角的度数,并说明理由.
相交所成的较小角的度数,并说明理由.
(3)解决问题:
如图3,当![]() 时,若
时,若![]() 是
是![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,且点
上,且点![]() 在同一条直线上,请直接写出
在同一条直线上,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条顶点坐标为![]() 的抛物线与y轴交于点C(0,5).与x轴交于点A和点B(点B在点A右侧),有一宽度为1.长崖足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q(点P在点Q右侧),交直线AC于点M和点N(点M在点N右侧),交x轴于点E和点F(点E在点F右侧)
的抛物线与y轴交于点C(0,5).与x轴交于点A和点B(点B在点A右侧),有一宽度为1.长崖足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q(点P在点Q右侧),交直线AC于点M和点N(点M在点N右侧),交x轴于点E和点F(点E在点F右侧)
(1)求抛物线的解析式;
(2)当点M和点N都在线段AC上时,连接MF,如果![]() ,求点Q的坐标;
,求点Q的坐标;
(3)在矩形平移的过程中,当以点P、Q、M、N为顶点的四边形是平行四边形时,直接写出点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com