
【题目】已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.

(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.
【答案】解:(1)证明:连接AC,
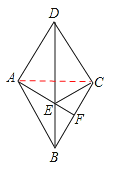
∵BD,AC是菱形ABCD的对角线,∴BD垂直平分AC。
∴AE=EC。
(2)点F是线段BC的中点。理由如下:
在菱形ABCD中,AB=BC,
又∵∠ABC=60°,∴△ABC是等边三角形。
∴∠BAC=60°。
∵AE=EC,∠CEF=60°,∴∠EAC=![]() ∠BAC=30°。
∠BAC=30°。
∴AF是△ABC的角平分线。
∵AF交BC于F,∴AF是△ABC的BC边上的中线。
∴点F是线段BC的中点。
【解析】
试题分析:(1)连接AC,根据菱形的对角线互相垂直平分可得BD垂直平分AC,再根据线段垂直平分线上的点到线段两端点的距离相等即可得证。
(2)先判定出△ABC是等边三角形,根据等边三角形的每一个角都是60°可得∠BAC=60°,再根据等边对等角以及三角形的一个外角等于与它不相邻的两个内角的和求出∠EAC=30°,从而判断出AF是△ABC的角平分线,再根据等边三角形的性质可得AF是△ABC的BC边上的中线,从而解得。


科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 一个正数的算术平方根一定是正数 B. 一个数的立方根一定比这个数小
C. 一个非零的数的立方根任然是一个非零的数 D. 负数没有平方根,但有立方根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面网格中每个小正方形的边长为1. 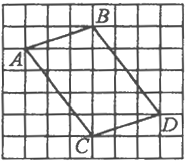
(1)线段CD是线段AB经过怎样的平移后得到的?
(2)线段AC是线段BD经过怎样的平移后得到的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在¨ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF,BF

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE, OP⊥CD,∠ABO=40°,则下列结论:①∠BO E=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有(填序号)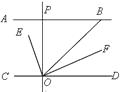
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com