
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮAOBCжаЃЌACЁЮOBЃЌЖЅЕуOЪЧдЕуЃЌЖЅЕуAЕФзјБъЮЊЃЈ0ЃЌ8ЃЉЃЌACЃН24cmЃЌOBЃН26cmЃЌЕуPДгЕуAГіЗЂЃЌвд1cm/sЕФЫйЖШЯђЕуCдЫЖЏЃЌЕуQДгЕуBЭЌЪБГіЗЂЃЌвд3m/sЕФЫйЖШЯђЕуOдЫЖЏЃЎЙцЖЈЦфжавЛИіЖЏЕуЕНДяЖЫЕуЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏЃЛДгдЫЖЏПЊЪМЃЌЩшPЃЈQЃЉЕудЫЖЏЕФЪБМфЮЊtsЃЎ
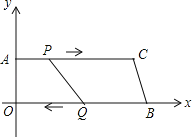
ЃЈ1ЃЉЧѓжБЯпBCЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌЫФБпаЮAOQPЪЧОиаЮЃП
ЁОД№АИЁП(1) yЃНЉ4x+104ЃЛ (2) ЕБtЮЊ6.5sЪБЃЌЫФБпаЮAOQPЪЧОиаЮ
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШИљОнЖЅЕуAЕФзјБъЮЊЃЈ0ЃЌ8ЃЉЃЌAC=24cmЃЌOB=26cmЃЌЗжБ№ЧѓГіЕуBЁЂCЕФзјБъИїЪЧЖрЩйЃЛШЛКѓгІгУД§ЖЈЯЕЪ§ЗЈЃЌЧѓГіжБЯпBCЕФКЏЪ§НтЮіЪНМДПЩЃЎ
ЃЈ2ЃЉИљОнЫФБпаЮAOQPЪЧОиаЮЃЌПЩЕУAP=OQЃЌОнДЫЧѓГіtЕФжЕЪЧЖрЩйМДПЩЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌ
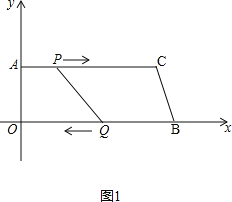
ЁпЖЅЕуAЕФзјБъЮЊЃЈ0ЃЌ8ЃЉЃЌACЃН24 cmЃЌOBЃН26 cmЃЌ
ЁрBЃЈ26ЃЌ0ЃЉЃЌCЃЈ24ЃЌ8ЃЉЃЌ
ЩшжБЯпBCЕФКЏЪ§НтЮіЪНЪЧyЃНkx+bЃЌ
дђ![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпBCЕФКЏЪ§НтЮіЪНЪЧyЃНЉ4x+104ЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌ
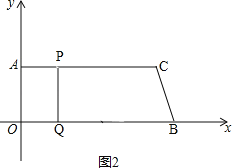
ИљОнЬтвтЕУЃКAPЃНt cmЃЌBQЃН3t cmЃЌдђOQЃНOBЉBQЃНЃЈ26Љ3tЃЉcmЃЌ
ЁпЫФБпаЮAOQPЪЧОиаЮЃЌ
ЁрAPЃНOQЃЌ
ЁрtЃН26Љ3tЃЌ
НтЕУtЃН6.5ЃЌ
ЁрЕБtЮЊ6.5sЪБЃЌЫФБпаЮAOQPЪЧОиаЮЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАыОЖЮЊ![]() ЕФ
ЕФ![]() жаЃЌЯв
жаЃЌЯв![]() ЃЌ
ЃЌ![]() ЫљЖдЕФдВаФНЧЗжБ№ЪЧ
ЫљЖдЕФдВаФНЧЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌдђЯв
ЃЌдђЯв![]() ЕФГЄЕШгкЃЈ ЃЉ
ЕФГЄЕШгкЃЈ ЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃН(xЃm)2Ѓ(xЃm)ЃЌЦфжаmЪЧГЃЪ§ЃЎ
(1)ЧѓжЄЃКВЛТлmЮЊКЮжЕЃЌИУХзЮяЯпгыxжсвЛЖЈгаСНИіЙЋЙВЕуЃЛ
(2)ШєИУХзЮяЯпЕФЖдГЦжсЮЊжБЯпxЃН![]() .
.
ЂйЧѓИУХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЂкАбИУХзЮяЯпбиyжсЯђЩЯЦНвЦЖрЩйИіЕЅЮЛГЄЖШКѓЃЌЕУЕНЕФХзЮяЯпгыxжсжЛгавЛИіЙЋЙВЕуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЁїABCжаЃЌЁЯABCЃН45ЁуЃЌAHЁЭBCгкЕуHЃЌЕуDЮЊAHЩЯЕФвЛЕуЃЌЧвDH=HCЃЌСЌНсBDВЂбгГЄBDНЛACгкЕуEЃЌСЌНсEHЃЎ

ЃЈ1ЃЉЧыВЙШЋЭМаЮЃЛ
ЃЈ2ЃЉжБНгаДГіBDгыACЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЃЛ
ЃЈ3ЃЉЧѓжЄЃКЁЯBEH=45ЁуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌДѓТЅ![]() ЃЈПЩвдПДзїВЛЭИУїЕФГЄЗНЬхЃЉЕФЫФжмЖМЪЧПеПѕЕФЫЎЦНЕиУцЃЎЕиУцЩЯгаМзЁЂввСНШЫЃЌЫћУЧЯждкЗжБ№ЮЛгкЕу
ЃЈПЩвдПДзїВЛЭИУїЕФГЄЗНЬхЃЉЕФЫФжмЖМЪЧПеПѕЕФЫЎЦНЕиУцЃЎЕиУцЩЯгаМзЁЂввСНШЫЃЌЫћУЧЯждкЗжБ№ЮЛгкЕу![]() КЭЕу
КЭЕу![]() ДІЃЌ
ДІЃЌ![]() ЁЂ
ЁЂ![]() Ољдк
Ољдк![]() ЕФжаДЙЯпЩЯЃЌЧв
ЕФжаДЙЯпЩЯЃЌЧв![]() ЁЂ
ЁЂ![]() ЕНДѓТЅЕФОрРыЗжБ№ЮЊ
ЕНДѓТЅЕФОрРыЗжБ№ЮЊ![]() УзКЭ
УзКЭ![]() УзЃЌгжвбжЊ
УзЃЌгжвбжЊ![]() ГЄ
ГЄ![]() УзЃЌ
УзЃЌ![]() ГЄ
ГЄ![]() УзЃЌгЩгкДѓТЅекЕВзХЃЌЫљвдввВЛФмПДЕНМзЃЎШєввбизХДѓТЅЕФЭтУцЕиДјаазпЃЌжБЕНПДЕНМзЃЈМзБЃГжВЛЖЏЃЉЃЌдђЫћаазпЕФзюЖЬОрРыГЄЮЊ________УзЃЎ
УзЃЌгЩгкДѓТЅекЕВзХЃЌЫљвдввВЛФмПДЕНМзЃЎШєввбизХДѓТЅЕФЭтУцЕиДјаазпЃЌжБЕНПДЕНМзЃЈМзБЃГжВЛЖЏЃЉЃЌдђЫћаазпЕФзюЖЬОрРыГЄЮЊ________УзЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌЁЯABDЁЂЁЯCDBЕФЦНЗжЯпBEЁЂDFЗжБ№НЛБпADЁЂBCгкЕуEЁЂFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮBEDFЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉЕБЁЯABEЮЊЖрЩйЖШЪБЃЌЫФБпаЮBEDFЪЧСтаЮЃПЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊAЁЂBЁЂCЁЂDЮЊОиаЮЕФЫФИіЖЅЕуЃЌAB=16cmЃЌAD=6cmЃЌЖЏЕуPЁЂQЗжБ№ДгЕуAЁЂCЭЌЪБГіЗЂЃЌЕуPвд3cm/sЕФЫйЖШЯђЕуBвЦЖЏЃЌЕуQвд2cm/sЕФЫйЖШЯђЕуDвЦЖЏЃЌЕБЕуPдЫЖЏЕНЕуBЭЃжЙЪБЃЌЕуQвВЫцжЎЭЃжЙдЫЖЏЃЌЮЪЃК
ЃЈ1ЃЉPЁЂQСНЕуДгПЊЪМГіЗЂЖрГЄЪБМфЪБЃЌЫФБпаЮPBCQЕФУцЛ§ЪЧ33![]() ЃП
ЃП
ЃЈ2ЃЉPЁЂQСНЕуДгПЊЪМГіЗЂЖрГЄЪБМфЪБЃЌЕуPгыQжЎМфЕФОрРыЪЧ10cmЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъЯЕдЕуЃЌОиаЮOABCЕФБпOAЃЌOCЗжБ№дкжсКЭжсЩЯЃЌЦфжаOA=6ЃЌOC=3ЃЎвбжЊЗДБШР§КЏЪ§![]() ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§BCБпЩЯЕФжаЕуDЃЌНЛABгкЕуEЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§BCБпЩЯЕФжаЕуDЃЌНЛABгкЕуEЃЎ
ЃЈ1ЃЉkЕФжЕЮЊ ЃЛ
ЃЈ2ЃЉВТЯыЁїOCDЕФУцЛ§гыЁїOBEЕФУцЛ§жЎМфЕФЙиЯЕЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПе§ЗНаЮЭјИёжаЃЌаЁИёЕФЖЅЕуНазіИёЕуЃЌвдИёЕуЮЊЖЅЕуЕФШ§НЧаЮНазіИёЕуШ§НЧаЮЃЎЯТЭМ![]() жаЕФе§ЗНаЮЭјИёжа
жаЕФе§ЗНаЮЭјИёжа![]() ЪЧИёЕуШ§НЧаЮЃЌаЁе§ЗНаЮЭјИёЕФБпГЄЮЊ
ЪЧИёЕуШ§НЧаЮЃЌаЁе§ЗНаЮЭјИёЕФБпГЄЮЊ![]() ЃЈЕЅЮЛГЄЖШЃЉЃЎ
ЃЈЕЅЮЛГЄЖШЃЉЃЎ
![]() ЕФУцЛ§ЪЧ________ЃЈЦНЗНЕЅЮЛЃЉЃЛ
ЕФУцЛ§ЪЧ________ЃЈЦНЗНЕЅЮЛЃЉЃЛ
![]() дкЭМ
дкЭМ![]() ЫљЪОЕФе§ЗНаЮЭјИёжазїГіИёЕу
ЫљЪОЕФе§ЗНаЮЭјИёжазїГіИёЕу![]() КЭ
КЭ![]() Ёх
Ёх![]() Ёх
Ёх![]() ЁхЃЌЪЙ
ЁхЃЌЪЙ![]() ЃЌ
ЃЌ![]() Ёх
Ёх![]() Ёх
Ёх![]() Ёх
Ёх![]() ЃЌЧв
ЃЌЧв![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ёх
Ёх![]() ЁхжаШЮвтСНЬѕЯпЖЮЕФГЄЖШЖМВЛЯрЕШЃЛ
ЁхжаШЮвтСНЬѕЯпЖЮЕФГЄЖШЖМВЛЯрЕШЃЛ
![]() дкЫљгагы
дкЫљгагы![]() ЯрЫЦЕФИёЕуШ§НЧаЮжаЃЌЪЧЗёДцдкУцЛ§ЮЊ
ЯрЫЦЕФИёЕуШ§НЧаЮжаЃЌЪЧЗёДцдкУцЛ§ЮЊ![]() ЃЈЦНЗНЕЅЮЛЃЉЕФИёЕуШ§НЧаЮЃПШчЙћДцдкЃЌЧыдкЭМ
ЃЈЦНЗНЕЅЮЛЃЉЕФИёЕуШ§НЧаЮЃПШчЙћДцдкЃЌЧыдкЭМ![]() жазїГіЃЌШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
жазїГіЃЌШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com