
【题目】如图,半径为![]() 的
的![]() 中,弦
中,弦![]() ,
,![]() 所对的圆心角分别是
所对的圆心角分别是![]() ,
,![]() ,若
,若![]() ,
,![]() ,则弦
,则弦![]() 的长等于( )
的长等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
作AH⊥BC于H,作直径CF,连结BF,先利用等角的补角相等得到∠DAE=∠BAF,然后再根据同圆中,相等的圆心角所对的弦相等得到DE=BF=6,由AH⊥BC,根据垂径定理得CH=BH,易得AH为△CBF的中位线,然后根据三角形中位线性质得到AH=![]() BF=3,从而求解.
BF=3,从而求解.
解:作AH⊥BC于H,作直径CF,连结BF,如图,
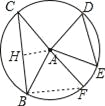
∵∠BAC+∠EAD=180°,而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,∴弧DE=弧BF,∴DE=BF=6,
∵AH⊥BC,∴CH=BH,
∵CA=AF,∴AH为△CBF的中位线,∴AH=![]() BF=3.
BF=3.
∴![]() ,
,
∴BC=2BH=8.
故选A.
“点睛”本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理和三角形中位线性质.


科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件。若商场平均每天要盈利1600元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=10cm,AD=8cm,点P从点A出发沿AB以2cm/s的速度向点终点B运动,同时点Q从点B出发沿BC以1cm/s的速度向点终点C运动,它们到达终点后停止运动.
(1)几秒后,点P、D的距离是点P、Q的距离的2倍;
(2)几秒后,△DPQ的面积是24cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC看,把AB点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠BAD+∠BCD=180°, AC平分∠BAD,过点C作CE⊥AD,垂足为E, CD=4,AE=10,则四边形ABCD的周长是____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形AOBC中,AC∥OB,顶点O是原点,顶点A的坐标为(0,8),AC=24cm,OB=26cm,点P从点A出发,以1cm/s的速度向点C运动,点Q从点B同时出发,以3m/s的速度向点O运动.规定其中一个动点到达端点时,另一个动点也随之停止运动;从运动开始,设P(Q)点运动的时间为ts.
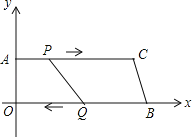
(1)求直线BC的函数解析式;
(2)当t为何值时,四边形AOQP是矩形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com