
【题目】如图,在矩形ABCD中,AB=10cm,AD=8cm,点P从点A出发沿AB以2cm/s的速度向点终点B运动,同时点Q从点B出发沿BC以1cm/s的速度向点终点C运动,它们到达终点后停止运动.
(1)几秒后,点P、D的距离是点P、Q的距离的2倍;
(2)几秒后,△DPQ的面积是24cm2.

【答案】(1)3;(2)4.
【解析】【试题分析】(1)设t秒后点P、D的距离是点P、Q距离的2倍,即PD=2PQ
因为四边形ABCD是矩形,根据矩形的性质得,∠A=∠B=90°利用勾股定理得:PD2=AP2+AD2 ,PQ2=BP2+BQ2,由于PD2=4 PQ2,即82+(2t)2=4[(10-2t)2+t2],
解得:t1=3,t2=7(舍去),即t=3;
(2) 设x秒后△DPQ的面积是24cm2,根据矩形的面积等于三个直角三角形的面积加上24,即![]()
x1=x2=4,即4秒后,△DPQ的面积是24cm2.
【试题解析】
(1)设t秒后点P、D的距离是点P、Q距离的2倍,
∴PD=2PQ
∵四边形ABCD是矩形
∴∠A=∠B=90°
∴PD2=AP2+AD2 ,PQ2=BP2+BQ2
∵PD2=4 PQ2,∴82+(2t)2=4[(10-2t)2+t2],
解得:t1=3,t2=7;
∵t=7时10-2t<0,∴t=3
(2) 设x秒后△DPQ的面积是24cm2,
∴![]()
整理得x2-8x+16=0
解得x1=x2=4
即4秒后,△DPQ的面积是24cm2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查(每位同学必选且只选一项)下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
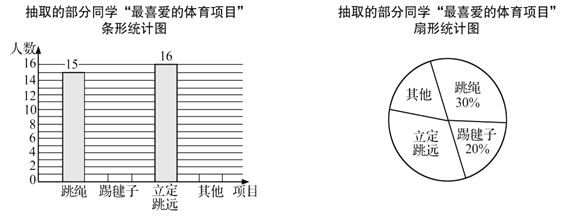
(1)小龙一共抽取了 名学生.
(2)补全条形统计图.
(3)求“立定跳远”部分对应的扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】符合下列条件之一的四边形不一定是菱形的是( )
A. 四条边相等
B. 两组邻边分别相等
C. 对角线相互垂直平分
D. 两条对角线分别平分一组对角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字2,1,﹣3,﹣4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从四张卡片中随机地摸取一张不放回,将该卡片上的数字记为m,再随机地摸取一张,将卡片上的数字记为n.
(1)请画出树状图并写出(m,n)所有可能的结果;
(2)求所选出的m,n能使一次函数y=mx+n的图象经过第二、三、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.(毛利润=(售价﹣进价)×销售量)
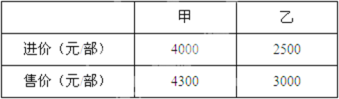
(1)该商场计划购进甲、乙两种手机各多少部?
(2) 通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com