
【题目】如图,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动,当点P运动到点B停止时,点Q也随之停止运动,问:
(1)P、Q两点从开始出发多长时间时,四边形PBCQ的面积是33![]() ?
?
(2)P、Q两点从开始出发多长时间时,点P与Q之间的距离是10cm?

【答案】(1) 5秒;(2) 4.8秒或1.6秒.
【解析】
(1)根据矩形和正方形的性质,利用梯形面积的求算方法,找出等量关系列出方程求解即可;
(2)作PE⊥CD,垂足为E,设运动时间为t秒,用t表示线段长,用勾股定理列方程求解.
(1)依题意得
AP=3t,
BP=AB-AP=16-3t,
CQ=2t,
DQ=DC-CQ=16-2t,
故S梯形PBCQ﹦![]() ﹙CQ+PB﹚BC.
﹙CQ+PB﹚BC.
又∵S梯形PBCQ﹦33,
∴![]() ﹙2t+16-3t﹚×6=33,
﹙2t+16-3t﹚×6=33,
解得t=5.
答:P、Q两点出发后5秒时,四边形PBCQ的面积为33cm2.
(2)过点P做PE⊥CD交CD于E.

QE=DQ-AP=16-5t,
在Rt△PQE中,
PE2+QE2=PQ2,
可得:(16-5t)2+62=102,
解得t1=4.8,t2=1.6.
故P、Q两点从开始出发4.8秒或1.6秒时,点P与Q之间的距离是10cm.


科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC看,把AB点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
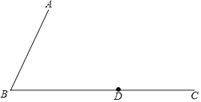
【题目】已知:如图,∠ABC,射线BC上一点D.
(1)求作:等腰△PBD,使线段BD为等腰△PBD的底边,点P在∠ABC内部,且点P到∠ABC两边的距离相等.
(2)在(1)的条件下,若DP⊥AB,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形AOBC中,AC∥OB,顶点O是原点,顶点A的坐标为(0,8),AC=24cm,OB=26cm,点P从点A出发,以1cm/s的速度向点C运动,点Q从点B同时出发,以3m/s的速度向点O运动.规定其中一个动点到达端点时,另一个动点也随之停止运动;从运动开始,设P(Q)点运动的时间为ts.
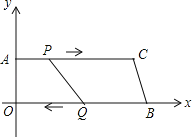
(1)求直线BC的函数解析式;
(2)当t为何值时,四边形AOQP是矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).

(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D为△ABC内一点, ∠BAD=15°,AD=AC,CE⊥AD于E,且CE=5.
(1)求BC的长;
(2)求证:BD=CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (k≠0)经过ABCD的顶点B、D,点A的坐标为(0,﹣1),AB∥x轴,CD经过点(0,2),ABCD的面积是18,则点D的坐标是( )
(k≠0)经过ABCD的顶点B、D,点A的坐标为(0,﹣1),AB∥x轴,CD经过点(0,2),ABCD的面积是18,则点D的坐标是( )

A. (﹣2,2) B. (3,2) C. (﹣3,2) D. (﹣6,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象上分别与x轴,y轴交于A、B两点,正比例函数的图象
的图象上分别与x轴,y轴交于A、B两点,正比例函数的图象![]() 与
与![]() 交于点
交于点![]() .
.
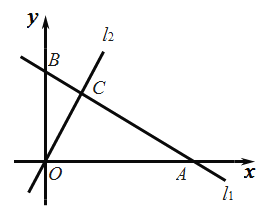
(1)求m的值;
(2)求直线![]() 的解析式;
的解析式;
(3)-次函数![]() 的图象为直线
的图象为直线![]() ,且
,且![]() ,
,![]() ,
,![]() 可以围成三角形,求k的取值范围.
可以围成三角形,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com