
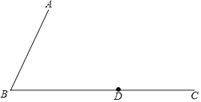
【题目】已知:如图,∠ABC,射线BC上一点D.
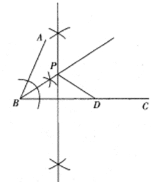
(1)求作:等腰△PBD,使线段BD为等腰△PBD的底边,点P在∠ABC内部,且点P到∠ABC两边的距离相等.
(2)在(1)的条件下,若DP⊥AB,求∠ABC的度数.
【答案】(1)作图见解析;(2)60°.
【解析】
(1)作∠ABC的平分线BK,线段BD的垂直平分线MN,射线BK与直线MN的交点P即为所求;
(2)根据DP⊥AB,可知![]() ,根据线段BD的垂直平分线MN,可知
,根据线段BD的垂直平分线MN,可知![]() 根据BP是∠ABC的平分线,可知
根据BP是∠ABC的平分线,可知![]() 等量代换可知
等量代换可知![]() 直角三角形两锐角互余,
直角三角形两锐角互余,![]() 从面求得∠ABC的度数.
从面求得∠ABC的度数.
(1)如图所示;点P是∠ABC的平分线与线段BD的垂直平分线的交点,如图点P即为所求;
(2) 在(1)的条件下,若DP⊥AB,如图:
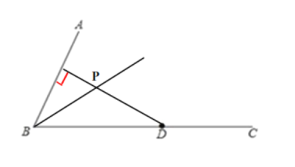
![]() 由(1)可知:∠ABC的平分线BK,线段BD的垂直平分线MN,射线BK与直线MN的交点P,
由(1)可知:∠ABC的平分线BK,线段BD的垂直平分线MN,射线BK与直线MN的交点P,
![]() (角平线的定义)
(角平线的定义)
![]() (垂直平分线的性质)
(垂直平分线的性质)
![]()
![]() DP⊥AB,
DP⊥AB,
![]()
![]() ,
,
且![]() (已证)
(已证)
![]()
![]() ,
,
![]()


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小方格的边长都为1,△![]() 各顶点都在格点上.若点
各顶点都在格点上.若点![]() 的坐标为(0,3),请按要求解答下列问题:
的坐标为(0,3),请按要求解答下列问题:
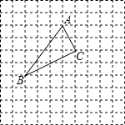
(1)在图中建立符合条件的平面直角坐标系;
(2)根据所建立的坐标系,写出点![]() 和点
和点![]() 的坐标;
的坐标;
(3)画出△![]() 关于
关于![]() 轴的对称图形△
轴的对称图形△![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=(x-m)2-(x-m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=![]() .
.
①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠ABC=45°,AH⊥BC于点H,点D为AH上的一点,且DH=HC,连结BD并延长BD交AC于点E,连结EH.

(1)请补全图形;
(2)直接写出BD与AC的数量关系和位置关系;
(3)求证:∠BEH=45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼![]() (可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点
(可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点![]() 和点
和点![]() 处,
处,![]() 、
、![]() 均在
均在![]() 的中垂线上,且
的中垂线上,且![]() 、
、![]() 到大楼的距离分别为
到大楼的距离分别为![]() 米和
米和![]() 米,又已知
米,又已知![]() 长
长![]() 米,
米,![]() 长
长![]() 米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.
米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动,当点P运动到点B停止时,点Q也随之停止运动,问:
(1)P、Q两点从开始出发多长时间时,四边形PBCQ的面积是33![]() ?
?
(2)P、Q两点从开始出发多长时间时,点P与Q之间的距离是10cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“欢乐跑中国重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了__分钟.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com