
����Ŀ�����������й�����վ������ǰϦ��С�պ�Сǿ��Լ�����ܲ���С�ձ�Сǿ��1�����ܲ����ţ�3���Ӻ��������������˺���2���Ӻ��������ܲ�����������ʱС�յ��ٶ�ʼ����180��/�֣�Сǿ���ٶ���220��/�֣�������ʼ10���Ӻ����������أ�Сǿͻ�����岻�ʣ���������ԭ·�Գ���ʱ���ٶȷ��أ�ֱ�������ٴ���������ͼ��ʾ��С�ա�Сǿ֮��ľ���y��ǧ�ף���С���ܲ�����ʱ��x�����ӣ�֮��ĺ���ͼ����С�մӼҳ����������ٴ�����ʱ��һ������__���ӣ�

���𰸡�![]()
������������: ��ͼ����Կ�����0-1min�ڣ�С�յ��ٶȿ��ɾ����С������ʱ����ã�1-3min�ڣ����ݵ�����ϵ�������С��=С���ܹ���·��+Сǿ�ܹ���·�����ɵó�Сǿ���ٶȣ�����С�յ��ٶ�ʼ����180��/�֣�Сǿ���ٶȿ�ʼ��220��/�֣������ǵ��ٶ�֮����40��/�֣���10�������400�ף����پ���t��������������������������õ�180t+120t=400��Ȼ�����t�����ǰ���15���ӿɵõ�С�մӼҳ����������ٴ�������ʱ���ܺͣ�
���: С�ձ���ǰ���ٶ�v1=��540-440��=100����/�֣���
��Сǿ����ǰ���ٶ�Ϊv2����/�֣���
���������2����v1+v2��=440�����v2=120��/�֣�
С�յ��ٶ�ʼ����180��/�֣�Сǿ���ٶȿ�ʼΪ220��/�֣����ǵ��ٶ�֮����40��/�֣�10�������400�ף�
���پ���t����������������180t+120t=400�����t=![]() ���֣�
���֣�
����С�մӼҳ����������ٴ�����ʱ5+10+![]() =
=![]() ���֣���
���֣���
�ʴ�Ϊ��![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
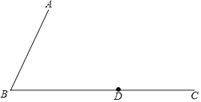
����Ŀ����֪����ͼ����ABC������BC��һ��D.
(1)������������PBD��ʹ�߶�BDΪ������PBD�ĵױߣ���P�ڡ�ABC�ڲ����ҵ�P����ABC���ߵľ������.
(2)��(1)�������£���DP��AB�����ABC�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����������y=![]() ��k��0������ABCD�Ķ���B��D����A������Ϊ��0����1����AB��x�ᣬCD�����㣨0��2����ABCD�������18�����D�������ǣ�������
��k��0������ABCD�Ķ���B��D����A������Ϊ��0����1����AB��x�ᣬCD�����㣨0��2����ABCD�������18�����D�������ǣ�������

A. ����2��2�� B. ��3��2�� C. ����3��2�� D. ����6��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�㣨��2��y1��������5![]() ��y2������1
��y2������1![]() ��y3���ں���y=2x2+8x+7��ͼ���ϣ���y1��y2��y3�Ĵ�С��ϵΪ_____��
��y3���ں���y=2x2+8x+7��ͼ���ϣ���y1��y2��y3�Ĵ�С��ϵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=��x2+bx+c��һֱ���ཻ��A����1��0����C��2��3�����㣬��y�ύ�ڵ�N���䶥��ΪD��
��1����������ֱ��AC�ĺ�����ϵʽ��
��2����P����������λ��ֱ��AC�Ϸ���һ�����㣬���APC����������ֵ����ʱ��P�����ꣻ
��3�����M��3��n������ʹMN+MDȡ��Сֵʱn��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��AD��BE����ABC�Ľ�ƽ���ߣ�D��E�ֱ���BC��AC�ϣ���AD=AB��BE=BC�����C=��������

A. 69�� B. ![]() C.
C. ![]() D. ����ȷ��
D. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���ֱ�ǡ�ABC�У���ACB=90�㣬CA=CB��CDΪб��AB�ϵ����ߣ�
��1����ͼ1��AEƽ�֡�CAB��BC��E����CD��F����DF=2����AC�ij���
��2����ͼ1�еġ�ADC�Ƶ�D˳ʱ����תһ���Ƕȵõ���ADN����ͼ2��P��Q�ֱ�Ϊ�߶�AN��BC���е㣬����AC��BN��PQ����֤��BN=![]() PQ��
PQ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ���Ϸֱ���x�ᣬy�ύ��A��B���㣬������������ͼ��
��ͼ���Ϸֱ���x�ᣬy�ύ��A��B���㣬������������ͼ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
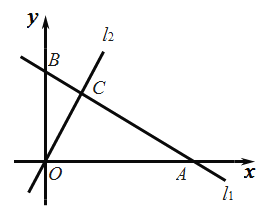
��1����m��ֵ��
��2����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��3��-�κ���![]() ��ͼ��Ϊֱ��
��ͼ��Ϊֱ��![]() ����
����![]() ��
��![]() ��
��![]() ����Χ�������Σ���k��ȡֵ��Χ��
����Χ�������Σ���k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x1��x2�ǹ���x��һԪ���η���4kx2��4kx��k��1��0������ʵ�������Ƿ����ʵ��k��ʹ(2x1��x2)(x1��2x2)����![]() �����������ڣ����k��ֵ���������ڣ���˵�����ɣ�
�����������ڣ����k��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com