
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0)、C(2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)设点M(3,n),求使MN+MD取最小值时n的值.

【答案】(1)y═﹣x2+2x+3,y=x+1;(2)P(![]() ,
,![]() );(3)
);(3)![]() .
.
【解析】
(1)利用待定系数法,以及点A(﹣1,0)、C(2,3)即可求得二次函数解析式、一次函数解析式;
(2)过点P作PQ⊥x轴交AC于点Q,交x轴于点H,设P(m,﹣m2+2m+3),,则点Q(m,m+1),则可求得线段PQ=﹣(m﹣![]() )2+
)2+![]() ,最后由图示以及三角形的面积公式表示出△APC 的面积,由二次函数最值的求法可知△APC的面积的最大值;
,最后由图示以及三角形的面积公式表示出△APC 的面积,由二次函数最值的求法可知△APC的面积的最大值;
(3)根据两点之间线段最短过点N作与直线x=3的对称点N′,连接DN′,,当M(3,n)在直线DN′上时,MN+MD的值最小.
(1)∵将点A和点C的坐标代入抛物线的解析式得:![]() ,
,
解得:b=2,c=3.
∴抛物线的解析式为y═﹣x2+2x+3.
设直线AC的解析式为y=kx+b.
∵将点A和点C的坐标代入得![]() ,解得k=1,b=1.
,解得k=1,b=1.
∴直线AC的解析式为y=x+1.
(2)如图,
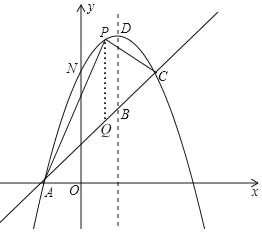
设点P(m,﹣m2+2m+3),
∴Q(m,m+1),
∴PQ=(﹣m2+2m+3)﹣(m+1)=﹣m2+m+2=﹣(m﹣![]() )2+
)2+![]() ,
,
∴S△APC=![]() PQ×|xC﹣xA|
PQ×|xC﹣xA|
=![]() [﹣(m﹣
[﹣(m﹣![]() )2+
)2+![]() ]×3=﹣
]×3=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
∴当m=![]() 时,S△APC最大=
时,S△APC最大=![]() ,y=﹣m2+2m+3=
,y=﹣m2+2m+3=![]() ,
,
∴P(![]() ,
,![]() );
);
(3)如图1所示,过点N作与直线x=3的对称点N′,连接DN′,交直线x=3与点M.
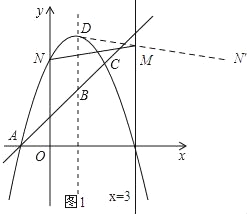
∵当x=0时y═3,
∴N(0,3).
∵点N与点N′关于x=3对称,
∴N′(6,3).
∵y═﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4).
设DN的解析式为y=kx+b.
将点N′与点D的坐标代入得:![]() ,
,
解得:k=﹣![]() ,b=
,b=![]() .
.
∴直线DN′的解析式为y=﹣![]() x+
x+![]() .
.
当x=3时,n=![]() +
+![]() =
=![]() .
.


科目:初中数学 来源: 题型:
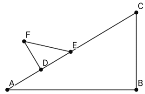
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图:在△ABC中,∠B=90°,∠A=30°,BC=5cm,等腰Rt△DEF中,∠FDE=![]() ,DE=3cm。动点D、E始终在边AB上,当点D从A点沿AC方向移动。
,DE=3cm。动点D、E始终在边AB上,当点D从A点沿AC方向移动。
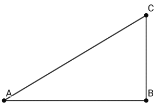
(1)在Rt△DEF沿AC方向移动的过程中,F,C两点之间的距离逐渐_______。(填“不变“变大”或“变小”)
(2)当F、C连线与AB平行时,求AD的长。
(3)以线段AD、FC、BC的长度为三边长的三角形是直角三角形时,求AD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 和直线
和直线![]() .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
下列判断: ①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x= 1 .
其中正确的有

A.1个 B.2个 C. 3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周的某一天,小王全家上午8时自驾小汽车从家里出发,到“番茄农庄”游玩,小汽车离家的距离![]() (千米)与小汽车离家后时间
(千米)与小汽车离家后时间![]() (时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:
(时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:

(1)“番茄农庄”离家________千米;
(2)小王全家在“番茄农庄”游玩了________小时;
(3)去时小汽车的平均速度是________千米/小时;
(4)回家时小汽车的平均速度是________千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“欢乐跑中国重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了__分钟.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),Rt△AOB中,∠A=90°,∠AOB=60°,OB=![]() ,∠AOB的平分线OC交AB于C,过O点做与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
,∠AOB的平分线OC交AB于C,过O点做与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
(1)求OC、BC的长;
(2)设△CPQ的面积为S,求S与t的函数关系式;
(3)当P在OC上Q在ON上运动时,如图(2),设PQ与OA交于点M,当t为何值时,△OPM为等腰三角形?求出所有满足条件的t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() :若由甲队先做20天,剩下的工程再由甲、乙两队合作60天完成.
:若由甲队先做20天,剩下的工程再由甲、乙两队合作60天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.6万元,乙队每天的施工费用为5.4万元,工程预算的施工费用为1000万元.若在甲、乙工程队工作效率不变的情况下使施工时间最短,问拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com