
【题目】如图,已知抛物线![]() 和直线
和直线![]() .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
下列判断: ①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x= 1 .
其中正确的有

A.1个 B.2个 C. 3个 D.4个
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且![]() +(a+2b-4)2=0.
+(a+2b-4)2=0.
(1)求a,b的值.
(2)在y轴的正半轴上存在一点M,使S△COM=![]() S△ABC,求出点M的坐标.
S△ABC,求出点M的坐标.
(3)在坐标轴的其他位置是否有在点M,使S△COM=![]() S△ABC仍成立?若存在,请直 接写出符合条件的点M的坐标.
S△ABC仍成立?若存在,请直 接写出符合条件的点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).

(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (k≠0)经过ABCD的顶点B、D,点A的坐标为(0,﹣1),AB∥x轴,CD经过点(0,2),ABCD的面积是18,则点D的坐标是( )
(k≠0)经过ABCD的顶点B、D,点A的坐标为(0,﹣1),AB∥x轴,CD经过点(0,2),ABCD的面积是18,则点D的坐标是( )

A. (﹣2,2) B. (3,2) C. (﹣3,2) D. (﹣6,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0)、C(2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)设点M(3,n),求使MN+MD取最小值时n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠ACB=90°,CA=CB,CD为斜边AB上的中线.
(1)如图1,AE平分∠CAB交BC于E,交CD于F,若DF=2,求AC的长;
(2)将图1中的△ADC绕点D顺时针旋转一定角度得到△ADN,如图2,P,Q分别为线段AN,BC的中点,连接AC,BN,PQ,求证:BN=![]() PQ.
PQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
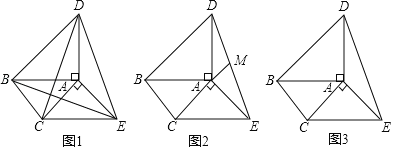
【题目】Rt△ABD和Rt△ACE如下3个图摆放,其中AB=AD,AC=AE.
(1)如图1,求证:BE=CD.
(2)如图2,M为DE中点,求证:BC=2AM.
(3)如图3,AB∥CE,AE∥BC,AC=![]() ,AB=2,直接写出四边形BCED的面积.
,AB=2,直接写出四边形BCED的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com